题目内容
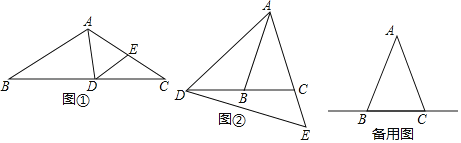
【题目】如图,在菱形![]() 中,
中,![]() 为边
为边![]() 的中点,
的中点,![]() 为边
为边![]() 上一动点(不与
上一动点(不与![]() 重合),将
重合),将![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,
,![]() ,当
,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长为____________.
的长为____________.
【答案】2 或![]()
【解析】
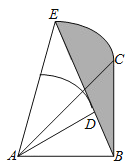
如图,分别以M、D为圆心,以DC为半径做圆.可以看出符合要求的点有A点与E’,两种情况,按两种情况分析即可.
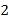
如图,分别以M、D为圆心,以DC为半径做圆.由于M是AB中点,四边形ABCD是菱形,结合图形所以,可以得出,符合要求的点有A点与E’,两种情况.
情况1:当E’与A点重合时,N与C重合,此时BN=AB
∵AB=2,四边形ABCD是菱形
∴BN=AB=2
情况2:作辅助线MP⊥AD于点P,连接AE’交MD于点H.
∵![]() ,四边形ABCD是菱形,
,四边形ABCD是菱形,![]() 为边
为边![]() 的中点
的中点
∴∠MAD=120°, AM=1
∴∠MAP=60°,
在Rt△APM中,解直角三角形
得: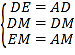
∴在Rt△ABE’中
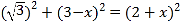
设BN=x
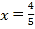
即:BN=![]()
综上所述BN为2或![]()

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
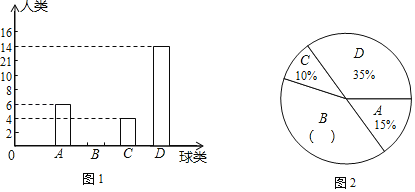
芒果教辅暑假天地重庆出版社系列答案【题目】今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(图11-1)和扇形统计图(图11-2),根据图表中的信息解答下列问题:
分组 | 分数段(分) | 频数 |
A | 36≤x<41 | 2 |
B | 41≤x<46 | 5 |
C | 46≤x<51 | 15 |
D | 51≤x<56 | m |
E | 56≤x<61 | 10 |

(1)求全班学生人数和![]() 的值.
的值.
(2)直接学出该班学生的中考体育成绩的中位数落在哪个分数段.
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.
【题目】弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下:
弹簧总长L(cm) | 16 | 17 | 18 | 19 | 20 |
重物质量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
(1)求L与x之间的函数关系;
(2)请估计重物为5kg时弹簧总长L(cm)是多少?