题目内容
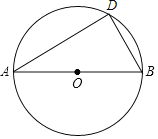
【题目】如图AB是⊙O的直径,点D为⊙O上任意一点连接AD,DB.
(1)在AD的上方作∠DAC=∠DAB,交劣弧AO于点C.(尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若∠DAB=30°,连接CD,OD.求证:四边形AODC为菱形.
【答案】(1)见解析(2)见解析
【解析】
(1)以D点为圆心,DB为半径画弧交⊙O于C,则C点满足条件;
(2)利用圆周角定理得到∠DOB=∠COD=60°,∠AOC=60°,则可判断△AOC和△COD都为等边三角形,所以OA=AC=CD=OD,然后根据菱形的判定方法可得到结论.
(1)解:如图,
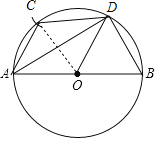
(2)证明:∵∠DAC=∠DAB=30°
∴∠DOB=∠COD=60°,
∴∠AOC=60°,
∴△AOC和△COD都为等边三角形
∴OA=AC=CD=OD,
∴四边形AODC为菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下:
弹簧总长L(cm) | 16 | 17 | 18 | 19 | 20 |
重物质量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
(1)求L与x之间的函数关系;
(2)请估计重物为5kg时弹簧总长L(cm)是多少?