题目内容
【题目】定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它的相关函数为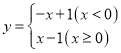 .
.
(1)已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;
(2)已知二次函数![]() .
.
①当点B(m,![]() )在这个函数的相关函数的图象上时,求m的值;
)在这个函数的相关函数的图象上时,求m的值;
②当﹣3≤x≤3时,求函数![]() 的相关函数的最大值和最小值;
的相关函数的最大值和最小值;
(3)在平面直角坐标系中,点M,N的坐标分别为(﹣![]() ,1),(
,1),(![]() ,1}),连结MN.直接写出线段MN与二次函数
,1}),连结MN.直接写出线段MN与二次函数![]() 的相关函数的图象有两个公共点时n的取值范围.
的相关函数的图象有两个公共点时n的取值范围.
【答案】(1)1;(2)①m=2﹣![]() 或m=2+
或m=2+![]() 或m=2﹣
或m=2﹣![]() ;②最大值为
;②最大值为![]() ,最小值为﹣
,最小值为﹣![]() ;(3)﹣3<n≤﹣1或1<n≤
;(3)﹣3<n≤﹣1或1<n≤![]() .
.
【解析】
试题(1)函数y=ax﹣3的相关函数为![]() ,将然后将点A(﹣5,8)代入y=﹣ax+3求解即可;
,将然后将点A(﹣5,8)代入y=﹣ax+3求解即可;
(2)二次函数![]() 的相关函数为
的相关函数为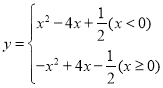 ,①分为m<0和m≥0两种情况将点B的坐标代入对应的关系式求解即可;②当﹣3≤x<0时,
,①分为m<0和m≥0两种情况将点B的坐标代入对应的关系式求解即可;②当﹣3≤x<0时,![]() ,然后可 此时的最大值和最小值,当0≤x≤3时,函数
,然后可 此时的最大值和最小值,当0≤x≤3时,函数![]() ,求得此时的最大值和最小值,从而可得到当﹣3≤x≤3时的最大值和最小值;
,求得此时的最大值和最小值,从而可得到当﹣3≤x≤3时的最大值和最小值;
(3)首先确定出二次函数![]() 的相关函数与线段MN恰好有1个交点、2个交点、3个交点时n的值,然后结合函数图象可确定出n的取值范围.
的相关函数与线段MN恰好有1个交点、2个交点、3个交点时n的值,然后结合函数图象可确定出n的取值范围.
试题解析:解:(1)函数y=ax﹣3的相关函数为![]() ,将点A(﹣5,8)代入y=﹣ax+3得:5a+3=8,解得:a=1.
,将点A(﹣5,8)代入y=﹣ax+3得:5a+3=8,解得:a=1.
(2)二次函数![]() 的相关函数为
的相关函数为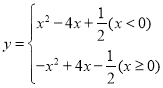 ;
;
①当m<0时,将B(m,![]() )代入
)代入![]() 得
得![]() ,解得:m=2+
,解得:m=2+![]() (舍去)或m=2﹣
(舍去)或m=2﹣![]() .
.
当m≥0时,将B(m,![]() )代入
)代入![]() 得:
得:![]() ,解得:m=2+
,解得:m=2+![]() 或m=2﹣
或m=2﹣![]() .
.
综上所述:m=2﹣![]() 或m=2+
或m=2+![]() 或m=2﹣
或m=2﹣![]() .
.
②当﹣3≤x<0时,![]() ,抛物线的对称轴为x=2,此时y随x的增大而减小,∴此时y的最大值为
,抛物线的对称轴为x=2,此时y随x的增大而减小,∴此时y的最大值为![]() .
.
当0≤x≤3时,函数![]() ,抛物线的对称轴为x=2,当x=0有最小值,最小值为﹣
,抛物线的对称轴为x=2,当x=0有最小值,最小值为﹣![]() ,当x=2时,有最大值,最大值y=
,当x=2时,有最大值,最大值y=![]() .
.
综上所述,当﹣3≤x≤3时,函数![]() 的相关函数的最大值为
的相关函数的最大值为![]() ,最小值为﹣
,最小值为﹣![]() ;
;
(3)如图1所示:线段MN与二次函数![]() 的相关函数的图象恰有1个公共点.
的相关函数的图象恰有1个公共点.
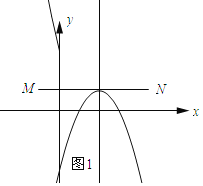
所以当x=2时,y=1,即﹣4+8+n=1,解得n=﹣3.
如图2所示:线段MN与二次函数![]() 的相关函数的图象恰有3个公共点
的相关函数的图象恰有3个公共点
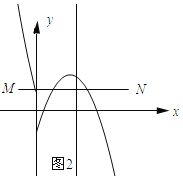
∵抛物线![]() 与y轴交点纵坐标为1,∴﹣n=1,解得:n=﹣1,∴当﹣3<n≤﹣1时,线段MN与二次函数
与y轴交点纵坐标为1,∴﹣n=1,解得:n=﹣1,∴当﹣3<n≤﹣1时,线段MN与二次函数![]() 的相关函数的图象恰有2个公共点.
的相关函数的图象恰有2个公共点.
如图3所示:线段MN与二次函数![]() 的相关函数的图象恰有3个公共点.
的相关函数的图象恰有3个公共点.
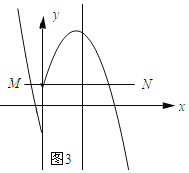
∵抛物线![]() 经过点(0,1),∴n=1.
经过点(0,1),∴n=1.
如图4所示:线段MN与二次函数![]() 的相关函数的图象恰有2个公共点.
的相关函数的图象恰有2个公共点.
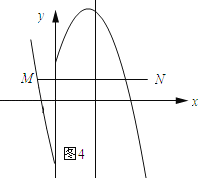
∵抛物线![]() 经过点M(﹣
经过点M(﹣![]() ,1),∴
,1),∴![]() +2﹣n=1,解得:n=
+2﹣n=1,解得:n=![]() ,∴1<n≤
,∴1<n≤![]() 时,线段MN与二次函数
时,线段MN与二次函数![]() 的相关函数的图象恰有2个公共点.
的相关函数的图象恰有2个公共点.
综上所述,n的取值范围是﹣3<n≤﹣1或1<n≤![]() .
.

 名校课堂系列答案
名校课堂系列答案