Question

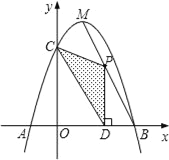
【题目】如图，已知抛物线y=ax2+bx+3过等腰Rt△BOC的两顶点B、C，且与x轴交于点A（﹣1，0）．

（1）求抛物线的解析式；

（2）抛物线的对称轴与直线BC相交于点M，点N为x轴上一点，当以M，N，B为顶点的三角形与△ABC相似时，求BN的长度；

（3）P为线段BC上方的抛物线上的一个动点，P到直线BC的距离是否存在最大值？若存在，请求出这个最大值的大小以及此时点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y=﹣x2+2x+3（2）3或（3）

【解析】

（1）令x=0，可得y=3，可得C点坐标为（0，3），根据等腰直角三角形的性质可得B点坐标为（3，0），即可利用待定系数法求得该抛物线的解析式．

（2）已知了B、C的坐标，易求得BC的长和直线BC的解析式，联立抛物线的对称轴即可得到点M的坐标，从而求得BM的长，可设出点BN=x，若以M，N，B为顶点的三角形与△ABC相似，由于∠CBA=∠MBN，则有两种情况需要考虑：①△MBN∽△CBA，②△MBN∽△ABC；根据上述两种情况所得不同的比例线段即可求得点N的坐标，进而可求出BN的长．

（3）可设经过P与直线BC平行的直线解析式为y=﹣x+n，联立方程y=﹣x2+2x+3，根据判别式为0得到n，从而得到经过P与直线BC平行的直线解析式，进一步得到点P的坐标，再根据待定系数法求得经过点P与直线BC垂直的直线解析式，联立直线BC的解析式得到交点坐标，再根据两点间的距离公式求解即可．

（1）令x=0，则y=3，∴C（0，3），∴OC=3．

又∵Rt△BOC是等腰直角三角形，∴B（3，0），将A（﹣1，0），B（3，0）代入y=ax2+bx+3得：，解得，∴y=﹣x2+2x+3．

（2）抛物线的对称轴为直线x=﹣=1，由B（3，0），C（0，3），得直线BC解析式为：y=﹣x+3；

∵对称轴x=1与直线BC：y=﹣x+3相交于点M，∴M为（1，2）；

可设BN的长为x．

当△MNB∽△ACB时，∴=，即=，解得：x=3；

当△MNB∽△CAB时，∴==，解得：x=，所以BN的长为3或．

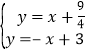（3）设经过P与直线BC平行的直线解析式为y=﹣x+n，联立得：，﹣x+n=﹣x2+2x+3，x2﹣3x+n﹣3=0，△=9﹣4（n﹣3）=0，解得：n=，∴P到直线BC的距离存在最大值时，经过P与直线BC平行的直线解析式为y=﹣x+，则x2﹣3x+=0，解得：x=，y=﹣+=，∴点P的坐标为（），则经过点P与直线BC垂直的直线解析式为y=x+t，则=+t，解得：t=，故经过点P与直线BC垂直的直线解析式为y=x+，联立可得，解得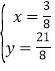：，则P到直线BC的距离最大值为=．