题目内容
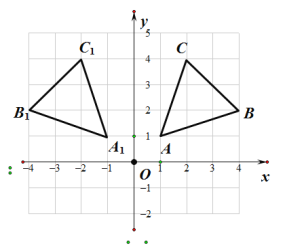
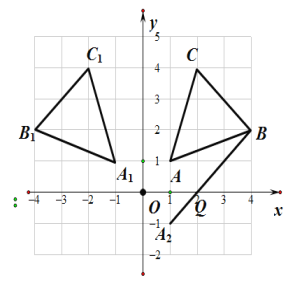
【题目】已知，在如图所示的网格中建立平面直角坐标系后，△ABC三个顶点的坐标分别为A（1，1）、B（4，2）、C（2，4）．
（1）画出△ABC关于y轴的对称图形△A1B1C1；
（2）借助图中的网格，请只用直尺（不含刻度）完成以下要求：
①在图中找一点P，使得P到AB、AC的距离相等，且PA＝PB；
②在x轴上找一点Q，使得△QAB的周长最小，并求出此时点Q的坐标．
【答案】（1）见详解；（2）①见详解；②
【解析】
（1）根据题意作出A,B,C关于y轴的对应点，顺次连接即可；
（2）①若P到AB、AC的距离相等，则P在
的平分线上；若PA＝PB，则P在AB的垂直平分线上，综合，P即为 的平分线与AB的垂直平分线的交点.
②先作出A关于x轴的对称点
，连接
，则直线与x轴的交点即为Q点.可用待定系数法求出直线的解析式，令
，可求Q的坐标.
（1）如图
（2）①如图
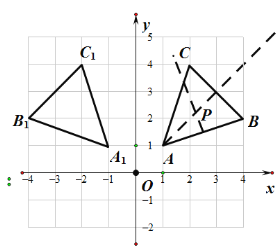
②如图
此时点
设直线的函数解析式为
，将代入中，得
解得
∴直线的函数解析式为
令，
练习册系列答案
相关题目
【题目】某班“数学兴趣小组”对函数y=|x|-2的图象特征进行了探究，探究过程如下：
⑴自变量x的取值范围是全体实数，x与y的几组对应值如下：
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 1 | m | -1 | -2 | n | 0 | 1 | 2 | … |
其中，m= ，n= .
⑵根据表中数据，在如图所示的平面直角坐标系中描点，并画出函数图象；
⑶观察函数图象，写出一条特征： .
