题目内容
【题目】通过对下面数学模型的研究学习，解决下列问题：
（模型呈现）
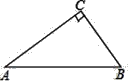
(1)如图1，
，
，过点
作
于点
，过点
作
于点
.由
，得
.又
，可以推理得到
.进而得到
_____，
_____.我们把这个数学模型称为“
字”模型或“一线三等角”模型；
（模型应用）
(2)①如图2，
，，
，连接
，
，且
于点
，与直线
交于点
.求证：点是的中点.
②如图3，在平面直角坐标系
中，点
为平面内任一点，点的坐标为
.若
是以
为斜边的等腰直角三角形，请直接写出点的坐标.
【答案】(1)DE，AE；(2)①证明见解析；②点A坐标为(
，
)或(，
).
【解析】
一线三等角必有全等三角形，通过等角的余角相等找对应关系求证全等即可.
(1)DE，AE；
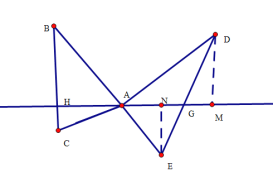
（2）①如图所示，作DM⊥HG于点M，作EN⊥HG于点N，则EN=HA，DM=HA.
∵∠ENG=∠DMG=90°，∠NGE=∠MGD，EN=DM=HA，
∴△ENG≌△PMG，
∴EG=GD，
∴G为ED中点.
③ 点A坐标为(，)或(，).
练习册系列答案
相关题目
【题目】某班“数学兴趣小组”对函数y=|x|-2的图象特征进行了探究，探究过程如下：
⑴自变量x的取值范围是全体实数，x与y的几组对应值如下：
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 1 | m | -1 | -2 | n | 0 | 1 | 2 | … |
其中，m= ，n= .
⑵根据表中数据，在如图所示的平面直角坐标系中描点，并画出函数图象；
⑶观察函数图象，写出一条特征： .
【题目】某校团委组织“阳光助残”献爱心捐款活动，九年级（2）班学生捐款如表：
捐款金额（元） | 5 | 10 | 15 | 20 |
人数（人） | 13 | 16 | 17 | 10 |
学生捐款的中位数和众数是（ ）
A. 10元，15元 B. 15元，15元 C. 10元，20元 D. 16元，17元
