题目内容
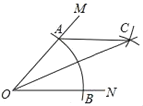
【题目】已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.

(1)若DF=2,求AB的长;
(2)若AB=18时,等边△CDP和△EFP的面积之和是否有最大值,如果有最大值,求最大值及此时P点位置,若没有最大值,说明理由.
【答案】(1)AB= 6;(2)没有最大值,理由见解析.
【解析】(1)由等边三角形的性质容易得出结果;
(2)设CD=PC=PD=x,则EF=EP=PF=6﹣x,求出等边△CDP和△EFP的面积之和S=![]() x2﹣3
x2﹣3![]() x+9
x+9![]() >0,得出S有最小值,没有最大值.
>0,得出S有最小值,没有最大值.
(1)∵△CDP和△EFP是等边三角形,∴CD=PC=PD,EF=EP=PF,AP=3PD,BP=3PF.
∵DF=PD+PF=2,∴AB=AP+BP=3DF=3×2=6;
(2)没有最大值,理由如下:
设CD=PC=PD=x,则EF=EP=PF=![]() (18﹣3x)=6﹣x,作CM⊥PD于M,EN⊥PF于N,则DM=
(18﹣3x)=6﹣x,作CM⊥PD于M,EN⊥PF于N,则DM=![]() PD=
PD=![]() x,PN=
x,PN=![]() PF=
PF=![]() (6﹣x),∴CM=
(6﹣x),∴CM=![]() DM=
DM=![]() x,EN=
x,EN=![]() (6﹣x),
(6﹣x),
∴△CDP的面积=![]() PDCM=
PDCM=![]() x2,△EFP的面积=
x2,△EFP的面积=![]() (6﹣x)2,
(6﹣x)2,
∴等边△CDP和△EFP的面积之和S=![]() x2+
x2+![]() (6﹣x)2=
(6﹣x)2=![]() x2﹣3
x2﹣3![]() x+9
x+9![]() .
.
∵![]() >0,∴S有最小值,没有最大值.
>0,∴S有最小值,没有最大值.


练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目