题目内容
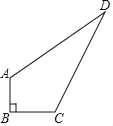
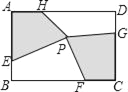
【题目】如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有_____.(填序号)

【答案】①②③④
【解析】分析:分别利用平行线的性质结合线段垂直平分线的性质以及等腰三角形的性质分别判断得出答案.
详解:∵BC=EC,
∴∠CEB=∠CBE,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CEB=∠EBF,
∴∠CBE=∠EBF,
∴①BE平分∠CBF,正确;
∵BC=EC,CF⊥BE,
∴∠ECF=∠BCF,
∴②CF平分∠DCB,正确;
∵DC∥AB,
∴∠DCF=∠CFB,
∵∠ECF=∠BCF,
∴∠CFB=∠BCF,
∴BF=BC,
∴③正确;
∵FB=BC,CF⊥BE,
∴B点一定在FC的垂直平分线上,即PB垂直平分FC,
∴PF=PC,故④正确.
故答案为①②③④.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目