Question

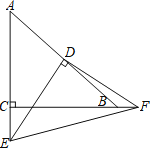
【题目】如图，已知Rt △ABC中，AC=BC，∠C=90°，D为AB边的中点，∠EDF=90°，∠EDF绕D点旋转，它的两边分别交AC、CB的延长线于E、F．下面结论一定成立的是______．（填序号）

①CD=AB；②DE=DF；③S△DEF=2S△CEF；④S△DEF-S△CEF=S△ABC．

Answer 1

【答案】①②

【解析】

连接CD，如图，利用直角三角形斜边上的中线性质可对①进行判断；再证明△CDE≌△BDF可对②进行判断；利用△DEF为等腰直角三角形得到根据三角形面积公式得到则可对③进行判断；然后计算则可对④进行判断．

解：连接CD，如图，

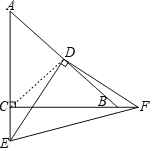
∵∠C=90°，D为AB边的中点，

∴CD=AD=DB，即 所以①正确；

∵CA=CB，∠C=90°，

∴∠ABC=45°，CD⊥BD，

∴∠DCE=135°，∠DBF=135°，

∵∠EDF=90°，

∴∠CDE=∠BDF，

在△CDE和△BDF中

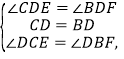
∴△CDE≌△BDF，

∴DE=DF，所以②正确；

∴△DEF为等腰直角三角形，

∴

∴

而EF2=CE2+CF2，

∴

而

∴

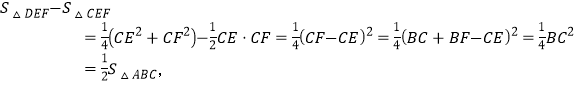
所以③④错误．

故答案为:①②．