题目内容
【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为18cm2,则S△DGF等于( )
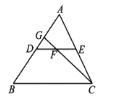
A.4cm2B.5cm2C.6cm2D.7 cm2
【答案】C
【解析】
取CG的中点H,连接EH,根据三角形的中位线定理可得EH∥AD,所以∠GDF=∠HEF,然后利用“角边角”证明△DFG和△EFH全等,所以FG=FH,S△EFH=S△DGF,易求出FC=3FH,再根据等高的三角形的面积比等于底边的比求出S△EFH,从而得解.
解:如图,取CG的中点H,连接EH,
∵E是AC的中点,
∴EH是△ACG的中位线,
∴EH∥AD,
∴∠GDF=∠HEF,
∵F是DE的中点,
∴DF=EF,
在△DFG和△EFH中,
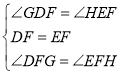
∴△DFG≌△EFH(ASA),
∴FG=FH,S△EFH=S△DGF ,
又∵FC=FH+HC=FH+GH=FH+FG+FH=3FH,
∴S△CEF=3S△EFH,
∴S△CEF=3S△DGF,
∴S△DGF=![]() ×18=6(cm2).
×18=6(cm2).
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目