Question

【题目】定义：当点C在线段AB上，AC=nAB时，我们称n为点C在线段AB上的点值，记作dC﹣AB=n．如点C是AB的中点时，即AC=AB，则dC﹣AB=；反过来，当dC﹣AB=时，则有AC=AB．

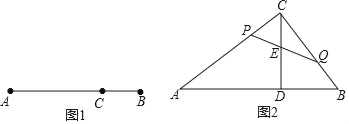
（1）如图1，点C在线段AB上，若dC﹣AB=，则=　 　；若AC=3BC，则dC﹣AB=　 　；

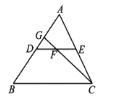
（2）如图2，在△ABC中，∠ACB=90°，CD⊥AB于点D，AB=10cm，BC=6cm，点P、Q分别从点C和点B同时出发，点P沿线段CA以2cm/s的速度向点A运动，点Q沿线段BC以1cm/s的速度向点C运动，当点P到达点A时，点P、Q均停止运动，连接PQ交CD于点E，设运动时间为ts，dP﹣CA+dQ﹣CB=m．

①当≤m≤时，求t的取值范围；

②当dP﹣CA=，求dE﹣CD的值；

③当dE﹣CD=时，求t的值．

Answer 1

【答案】（1），；（2）①3≤t≤4；②0.6；③t的值为2.4或

【解析】分析：（1）当点C在线段AB上，AC=nAB时，我们称n为点C在线段AB上的点值，记作dC-AB=n，据此进行判断即可；
（2）①根据dP-CA=，dQ-CB=，即可得到m=dP-CA+dQ-CB=，再根据，即可得到不等式，进而解得3≤t≤4；
②根据dP-CA=，dP-CA+dQ-CB=m，可得dP-CA=dQ-CB，即，进而得出，求得t=2.4，再根据，∠ACB=∠PCQ，判定△ACB∽△PCQ，进而得到PQ∥AB，得出，即可得到dE-CD=dP-CA==0.6；
③分两种情况：当PQ∥AB时，则有dE-CD=dP-CA=dQ-CB=，由②可得，t=2.4；当PQ与AB不平行时，过点P，Q分别作PM⊥CD于点M，QN⊥CD于点N，根据dE-CD=，dP-CA+dQ-CB=m，推理可得△PME≌△QNE，即可得出PM=QN，最后根据PM=PC×sin∠ACD=2t×sin∠B=，QN=QC×sin∠BCD=（6-t）sin∠A=（6-t），得到关于t的方程，即可得出t=．

详解：（1）∵点C在线段AB上，若dC﹣AB=，

∴AC=AB，即=；

∵AC=3BC，

∴AC=AB，即dC﹣AB=，

故答案为：，；

（2）①在△ABC中，∠ACB=90°，AB=10，BC=6，

∴AC=8，

∵dP﹣CA==，dQ﹣CB==1﹣，

∴m=dP﹣CA+dQ﹣CB=+1﹣，

又∵≤m≤，

∴≤+1﹣≤，

解得3≤t≤4；

②∵dP﹣CA=，dP﹣CA+dQ﹣CB=m，

∴dP﹣CA=dQ﹣CB，

∴=，

∴=，

解得t=2.4，

∵=，∠ACB=∠PCQ，

∴△ACB∽△PCQ，

∴∠A=∠CPQ，

∴PQ∥AB，

∴=，

∴dE﹣CD=dP﹣CA==0.6；

③分两种情况：

当PQ∥AB时，则有dE﹣CD=dP﹣CA=dQ﹣CB=，

由②可得，t=2.4；

当PQ与AB不平行时，过点P，Q分别作PM⊥CD于点M，QN⊥CD于点N，如图所示，

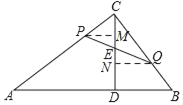
则有PM∥QN∥AB，且点M，N，E不重合，

∴=， =，

∵dE﹣CD=，dP﹣CA+dQ﹣CB=m，

∴dP﹣CA+dQ﹣CB=2dE﹣CD，

∴+=2，即+=2，

∴CM+CN=2CE，即点E是MN的中点，

∴EN=EM，

又∵∠PME=∠QNE，∠PEM=∠QEN，

∴△PME≌△QNE，

∴PM=QN，

∵PM=PC×sin∠ACD=2t×sin∠B=，QN=QC×sin∠BCD=（6﹣t）sin∠A=（6﹣t），

∴=（6﹣t），

解得t=，

综上所述，t的值为2.4或．