Question

【题目】阅读下面材料：小明遇到这样一个问题:

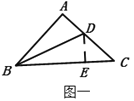
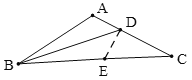
如图一，△ABC中，∠A=90°，AB=AC，BD平分∠ABC，猜想线段AD与DC数量关系.小明发现可以用下面方法解决问题:作DE⊥BC交BC于点E：

(1)根据阅读材料可得AD与DC的数量关系为__________.

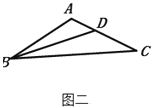
(2)如图二，△ABC中，∠A=120°，AB=AC，BD平分∠ABC，猜想线段AD与DC的数量关系，并证明你的猜想.

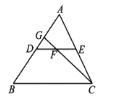
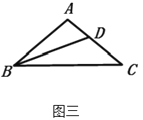
(3)如图三，△ABC中，∠A=100°，AB=AC，BD平分∠ABC，猜想线段AD与BD、BC的数量关系，并证明你的猜想.

Answer 1

【答案】（1）CD=AD；（2）CD=AD；（3）BC=AD+BD.

【解析】

（1）由角平分线的性质可得AD=DE，根据∠A=90°，AB=AC，可得∠C=45°，由DE⊥BC可得△DEC是等腰直角三角形，可得CD=DE，进而可得答案；（2）在BC上截取BE=AB，连接DE，利用SAS可证明△ABD≌△EBD，可得AD=DE，∠BED=∠A=120°，由等腰三角形的性质可得∠C=30°，利用三角形外角性质可得∠CDE=90°，利用含30°角的直角三角形的性质即可得答案；（3）在BC上取一点E，使BE=BD，作DF⊥BA于F，DG⊥BC于G，由角平分线的性质就可以得出DF=DG，利用AAS可证明△DAF≌△DEG，可得 DA=DE，利用外角性质可求出∠EDC=40°，进而可得DE=CE，即可得出结论．

（1）∵∠A=90°，BD平分∠ABC，DE⊥BC，

∴DE=AD，

∵∠A=90°，AB=AC，

∴∠C=45°，

∴△CDE是等腰直角三角形，

∴CD=DE=AD，

故答案为：CD=AD

（2）如图，在BC上截取BE=AB，连接DE，

∵BD平分∠ABC，

∴∠ABD=∠DBE，

在△ABD和△EBD中，，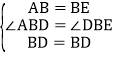

∴△ABD≌△EBD，

∴DE=AD，∠BED=∠A=120°，

∵AB=AC，

∴∠C=∠ABC=30°，

∴∠CDE=∠BED-∠C=90°，

∴CD=DE=AD.

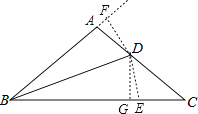
（3）如图，在BC上取一点E，是BE=BD，作DF⊥BA于F，DG⊥BC于G，

∴∠DFA=∠DGE=90°．

∵BD平分∠ABC，DF⊥BA，DG⊥BC，

∴DF=DG．

∵∠BAC=100°，AB=AC，

∴∠FAD=80°，∠ABC=∠C=40°，

∴∠DBC=20°，

∵BE=BD，

∴∠BED=∠BDE=80°，

∴∠FAD=∠BED．

在△DAF和△DEG中，，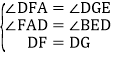

∴△DAF≌△DEG（AAS），

∴AD=ED．

∵∠BED=∠C+∠EDC，

∴80°=40+∠EDC，

∴∠EDC=40°，

∴∠EDC=∠C，

∴DE=CE，

∴AD=CE．

∵BC=BE+CE，

∴BC=BD+AD．