题目内容
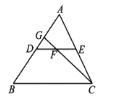
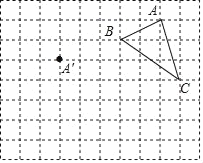
【题目】如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,则AF的最小值是_____.
【答案】3![]() ﹣1.
﹣1.
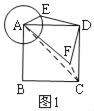
【解析】分析:先找出AF最大值时,点E的位置,再判断出AF最大时,点C在AF上,根据正方形的性质求出AC,从而得出AF的最大值.
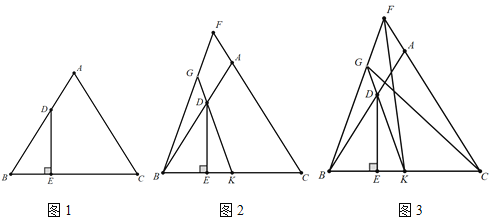
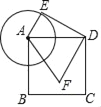
详解:如图1,连接FC,AF,
∵ED⊥DF,
∴∠EDF=∠EDA+∠ADF=90°,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADF+∠CDF=90°,
∴∠EDA=∠CDF,
在△ADE和△CDF中,
∵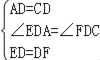 ,
,
∴△ADE≌△CDF,
∴CF=AE=1,
∴AF>AC﹣CF,即AF>AC﹣1,
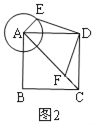
∴当F在AC上时,AF最小,如图2,
∵正方形ABCD的边长为3,
∴AC=3![]() ,
,
∴AF的最小值是3![]() ﹣1;
﹣1;
故答案为:3![]() ﹣1.
﹣1.

练习册系列答案
相关题目
【题目】“五一”期间,文具店老板购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 14 |
B型 | 15 | 22 |
(1)老板如何进货,能使进货款恰好为1350元?
(2)要使销售文具所获利润不少于500元,那么老板最多能购进A型文具多少只?
【题目】生态公园计划在园内的坡地上造一片有![]() 、
、![]() 两种树的混合林,需要购买这两种树苗2000棵,种植
两种树的混合林,需要购买这两种树苗2000棵,种植![]() 、
、![]() 两种树苗的相关信息如下表:
两种树苗的相关信息如下表:
品名 | 单价(元/棵) | 栽树劳务费(元/棵) | 成活率 |
| 25 | 3 |
|
| 30 | 4 |
|
设购买![]() 种树苗
种树苗![]() 棵,解答下列问题:
棵,解答下列问题:
(1)购买的![]() 种树苗的数量为_______棵(含
种树苗的数量为_______棵(含![]() 的代数式表示);
的代数式表示);
(2)请用含![]() 的代数式表示造这片林的总费用;
的代数式表示造这片林的总费用;
(3)假设这批树苗种植后成活1960棵,则造这片林的总费用需多少元?