题目内容
【题目】在矩形ABCD中，AB=3，AD=4，动点P从点B出发，以每秒1个单位的速度，沿BA向点A移动；同时点Q从点C出发，以每秒2个单位的速度，沿CB向点B移动，连接QP，QD，PD．若两个点同时运动的时间为x秒（0<x≤2），解答下列问题：
（1）当x为何值时，PQ⊥DQ；
（2）设△QPD的面积为S，用含x的函数关系式表示S；当x为何值时，S有最小值？并求出最小值．
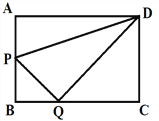
【答案】（1）1.25（2）当x=1.5时，S有最小值为3.75
【解析】分析：（1）可知
先判定
得到
即
解出x的值即得答案.
用矩形的面积减去三个直角三角形的面积即可表示出
，根据二次函数的性质求解即可.
详解：（1）当
时，
又∵四边形ABCD是矩形，
∴
∴
∴
，
∴
∴即
得
（2）
∴当
时，S有最小值为3.75.
练习册系列答案
相关题目
【题目】某校为了做好大课间活动，计划用400元购买10件体育用品，备选体育用品及单价如下表（单位：元）
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价（元） | 50 | 40 | 25 |
（1）若400元全部用来购买篮球和羽毛球拍共10件，问篮球和羽毛球拍各购买多少件？
（2）若400元全部用来购买篮球、排球和羽毛球拍三种共10件，能实现吗？（若能实现直接写出一种答案即可，若不能请说明理由.）
【题目】“五一”期间，文具店老板购进100只两种型号的文具进行销售，其进价和售价之间的关系如下表：
型号 | 进价（元/只） | 售价（元/只） |
A型 | 10 | 14 |
B型 | 15 | 22 |
（1）老板如何进货，能使进货款恰好为1350元？
（2）要使销售文具所获利润不少于500元，那么老板最多能购进A型文具多少只？
