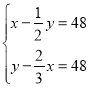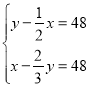题目内容
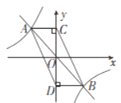
【题目】如图，函数y=－x与函数y=－
的图象相交于A、B两点，分别过A、B两点作y轴的垂线，垂足分别为点C、D，则四边形ACBD的面积为____________．
【答案】12
【解析】
首先根据反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
|k|，得出S△AOC=S△ODB=3，再根据反比例函数的对称性可知OA=OB，即可求出四边形ACBD的面积．
解：∵过函数y=-
的图象上A，B两点分别作y轴的垂线，垂足分别为点C，D，
∴S△AOC=S△ODB=|k|=3，A、B关于原点对称
∴OA=OB，
∴S△AOC=S△ODA=S△ODB=S△OBC=3，
∴四边形ACBD的面积为：S△AOC+S△ODA+S△ODB+S△OBC=4×3=12．
故答案为：12．
练习册系列答案
相关题目
【题目】2018年非洲猪瘟疫情暴发后，专家预测，2019年我市猪肉售价将逐月上涨，每千克猪肉的售价y1（元）与月份x（1≤x≤12，且x为整数）之间满足一次函数关系，如下表所示．每千克猪肉的成本y2（元）与月份x（1≤x≤12，且x为整数）之间满足二次函数关系，且3月份每千克猪肉的成本全年最低，为9元，如图所示．
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |
（1）求y1与x之间的函数关系式．
（2）求y2与x之间的函数关系式．
（3）设销售每千克猪肉所获得的利润为w（元），求w与x之间的函数关系式，哪个月份销售每千克猪肉所第获得的利润最大？最大利润是多少元？
