题目内容
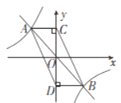
【题目】如图,在直角坐标系中,点![]() ,点
,点![]() ,过点
,过点![]() 的直线
的直线![]() 垂直于线段
垂直于线段![]() ,点
,点![]() 是直线
是直线![]() 上在第一象限内的一动点,过点
上在第一象限内的一动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,把
,把![]() 沿
沿![]() 翻折
翻折![]() ,使点
,使点![]() 落在点
落在点![]() 处,若以
处,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与△ABP相似,则满足此条件的点
为顶点的三角形与△ABP相似,则满足此条件的点![]() 的坐标为__________.
的坐标为__________.

【答案】![]() 或
或![]()
【解析】
求出直线l的解析式,证出△AOB∽△PCA,得出![]() ,设AC=m(m>0),则PC=2m,根据△PCA≌△PDA,得出
,设AC=m(m>0),则PC=2m,根据△PCA≌△PDA,得出 ![]() ,当△PAD∽△PBA时,根据
,当△PAD∽△PBA时,根据![]() ,
,![]() ,得出m=2,从而求出P点的坐标为(4,4)、(0,-4),若△PAD∽△BPA,得出
,得出m=2,从而求出P点的坐标为(4,4)、(0,-4),若△PAD∽△BPA,得出![]() ,求出
,求出![]() ,从而得出
,从而得出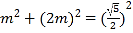 ,求出
,求出![]() ,即可得出P点的坐标为
,即可得出P点的坐标为![]() .
.
∵点A(2,0),点B(0,1),
∴直线AB的解析式为y=-![]() x+1
x+1
∵直线l过点A(4,0),且l⊥AB,
∴直线l的解析式为;y=2x-4,∠BAO+∠PAC=90°,
∵PC⊥x轴,
∴∠PAC+∠APC=90°,
∴∠BAO=∠APC,
∵∠AOB=∠ACP,
∴△AOB∽△PCA,
∴![]() ,
,
∴![]() ,
,
设AC=m(m>0),则PC=2m,
∵△PCA≌△PDA,
∴AC=AD,PC=PD,
∴![]() ,
,
如图1:当△PAD∽△PBA时,
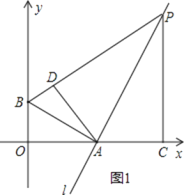
则![]() ,
,
则![]() ,
,
∵AB=![]() ,
,
∴AP=2![]() ,
,
∴![]() ,
,
∴m=±2,(负失去)
∴m=2,
当m=2时,PC=4,OC=4,P点的坐标为(4,4),
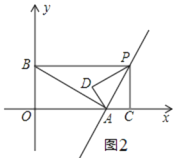
如图2,若△PAD∽△BPA,
则![]() ,
,
∴![]() ,
,
则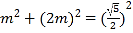 ,
,
∴m=±![]() ,(负舍去)
,(负舍去)
∴m=![]() ,
,
当m=![]() 时,PC=1,OC=
时,PC=1,OC=![]() ,
,
∴P点的坐标为(![]() ,1),
,1),
故答案为:P(4,4),P(![]() ,1).
,1).

练习册系列答案
相关题目