Question

【题目】在△ABC中，∠ABC＝90°，

（1）如图1，分别过A，C两点作经过点B的直线的垂线，垂足分别为M、N，求证：△ABM～△BCN；

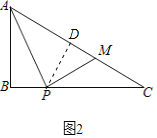
（2）如图2，P是边BC上一点，∠BAP＝∠C，PM⊥PA交AC于点M，＝，求的值；

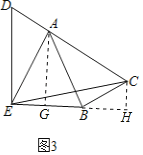
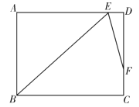
（3）如图3，D是边CA延长线上一点，AE＝AB，∠DEB＝90°，AD：BC：AC＝2：3：5，求的长．

Answer 1

【答案】（1）见解析；（2）；（3）

【解析】

（1）根据同角的余角相等得到∠MAB＝∠NBC，根据两角对应相等的两个三角形相似证明结论；

（2）过点P作PD⊥AM于D．证明△PDM∽△APM，根据相似三角形的性质得到，设DM＝2a，根据勾股定理求出PM，证明△CDP∽△CBA，根据相似三角形的性质解答即可；

（3）根据平行线的性质得到，根据相似三角形的性质得到，设BG＝4m，AG＝4n，根据求出n＝2m，计算即可．

（1）证明：∵AM⊥MN，

∴∠MAB+∠MBA＝90°，

∵∠ABC＝90°，

∴∠CBN+∠MBA＝90°，

∴∠MAB＝∠NBC，又∠AMB＝∠BNC＝90°，

∴△ABM～△BCN；

（2）解：过点P作PD⊥AM于D．

∴∠BAP+∠APB＝∠CPM+∠APB＝90°，

∴∠BAP＝∠CPM＝∠C，

∴MP＝MC，

∵PM⊥PA，PD⊥AM，

∴△PDM∽△APM，

∵

设DM＝2a，则

由勾股定理得，

∴CD＝DM+CM＝DM+PM＝5a

则

∵∠CDP＝∠CBA＝90°，∠C＝∠C，

∴△CDP∽△CBA，

∴

（3）解：过点A作AG⊥BE于G，过点C作CH⊥BE交EB的延长线于H，

∵∠DEB＝90°，

∴CH∥AG∥DE，

∴

∵BC：AC＝3：5，

∴BC：AB＝3：4，

由（1）可知，△ABG∽△BCH，

∴

设BG＝4m，CH＝3m，AG＝4n，BH＝3n，

∵AB＝AE，AG⊥BE，

∴EG＝BG＝4m，

∴GH＝BG+BH＝4m+3n，

∵

∴

解得，n＝2m，

AG＝4n＝8m，BH＝3n＝6m，

由勾股定理得

BE＝2BG＝8m，

∴