题目内容
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2m2x+2交y轴于点A,交直线x=4于点B.
(1)抛物线的对称轴为x=____________(用含m的代数式表示)
(2)若AB∥x轴,求抛物线的解析式.
(3)记抛物线在A、B之间的部分为图象G(包含A、B两点),若对于图象G上任意一点P(xp,yp),都有yp≤2,求m的取值范围.
【答案】(1)m(2)y=2x2-8x+2(3)m<0或m≥2
【解析】
(1)根据抛物线的对称轴为直线x=-![]() ,代入数据即可得出结论;
,代入数据即可得出结论;
(2)由AB∥x轴,可得出点B的坐标,进而可得出抛物线的对称轴为x=2,结合(1)可得出m=2,将其代入抛物线表达式中即可;
(3)分m>0及m<0两种情况考虑,依照题意画出函数图象,利用数形结合即可得出m的取值范围.
解:(1)抛物线的对称轴为![]()
故答案为:m.
(2)当x=0时,y=mx2-2m2x+2=2,
∴点A(0,2).
∵AB∥x轴,且点B在直线x=4上,
∴点B(4,2),抛物线的对称轴为直线x=2,
∴m=2,
∴抛物线的表达式为y=2x2-8x+2.
(3)当m>0时,如图1.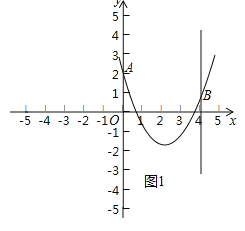
∵A(0,2),
∴要使0≤xp≤4时,始终满足yp≤2,只需使抛物线y=mx2-2m2x+2的对称轴与直线x=2重合或在直线x=2的右侧.
∴m≥2;
当m<0时,如图2,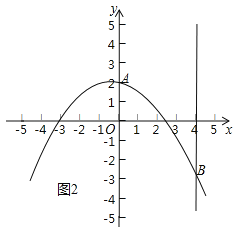
在0≤xp≤4中,yp≤2恒成立.
综上所述,m的取值范围为m<0或m≥2.

练习册系列答案
相关题目