题目内容
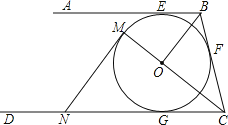
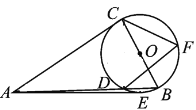
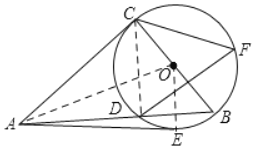
【题目】如图，Rt△ABC中，∠ACB＝90°，以BC为直径的⊙O交AB于点D，E、F是⊙O上的两点，连结AE、CF、DF，满足EA＝CA.
(1)求证：AE是⊙O的切线；
(2)若⊙O的半径是3，tan∠CFD＝
，求AD的长．
【答案】（1）证明见解析；（2）
.
【解析】
（1）连接OA，OE，易证△AOC≌△AOE（SSS），从而可知∠OEA=∠ACB=90°，所以AE是⊙O的切线．
（2）连接CD，因为∠CBA=∠CFD，所以tan∠CBA=tan∠CFD=
，从而可求出AC=8，利用勾股定理即可求出AB=10，再证明△ADC∽△ACB，从而可求出AD的长度．
（1）连接OA，OE，
在△AOC与△AOE中，
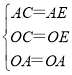
∴△AOC≌△AOE（SSS）
∴∠OEA=∠ACB=90°，
∴OE⊥AE，
∴AE是⊙O的切线
（2）连接CD
∵∠CBA=∠CFD
∴tan∠CBA=tan∠CFD=，
∵在Rt△ACB中，
tan∠CBA=
∴AC=8
∴由勾股定理可知：AB=10，
∵BC为⊙O的直径，
∴∠CDB=∠ADC=90°，
∵∠ADC=∠ACB，∠DAC=∠CAB，
∴△ADC∽△ACB
∴
，
∴AD=6.4
练习册系列答案
世纪百通期末金卷系列答案
相关题目
