题目内容
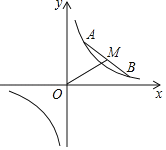
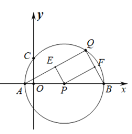
【题目】如图,一次函数y=kx+b(b=0)的图象与反比例函数y=![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣3,4),点B的坐标为(6,n)
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣3,4),点B的坐标为(6,n)

(1)求反比例函数和一次函数的解析式;
(2)连接OB,求△AOB的面积;
(3)若kx+b<![]() ,直接写出x的取值范围.
,直接写出x的取值范围.
【答案】(1)![]() ,y=﹣
,y=﹣![]() x+2;(2)9;(3)x>6或﹣3<x<0
x+2;(2)9;(3)x>6或﹣3<x<0
【解析】
(1)根据A的坐标求出反比例函数的解析式,求出B点的坐标,再把A、B的坐标代入y=kx+b,求出一次函数的解析式即可;
(2)先求出点C的坐标,再根据三角形的面积公式求出即可;
(3)根据A、B的坐标和图象得出即可.
解:(1)把A点的坐标(﹣3,4)代入y=![]() 得:m=﹣12,
得:m=﹣12,
即反比例函数的解析式是y=![]() ,
,
把B点的坐标(6,n)代入y=﹣![]() 得:n=﹣2,
得:n=﹣2,
即B点的坐标是(6,﹣2),
把A、B的坐标代入y=kx+b得:![]() ,
,
解得:k=﹣![]() ,b=2,
,b=2,
所以一次函数的解析式是y=﹣![]() x+2;
x+2;

(2)设一次函数y=﹣![]() x+2与x轴的交点是C,
x+2与x轴的交点是C,
y=﹣![]() x+2,当y=0时,x=3,
x+2,当y=0时,x=3,
即OC=3,
∵A(﹣3,4),B(6,﹣2),
∴△AOB的面积S=S△AOC+S△BOC=![]() =9;
=9;
(3)当kx+b<![]() 时x的取值范围是x>6或﹣3<x<0.
时x的取值范围是x>6或﹣3<x<0.

 名校课堂系列答案
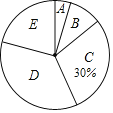
名校课堂系列答案【题目】某校九年级学生参加了中考体育考试.为了了解该校九年级(1)班同学的中考体育成绩情况,对全班学生的中考体育成绩进行了统计,并绘制出以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
分组 | 分数段(分) | 频数 |
A | 36≤x<41 | 2 |
B | 41≤x<46 | 5 |
C | 46≤x<51 | 15 |
D | 51≤x<56 | m |
E | 56≤x<61 | 10 |
(1)m的值为 ;
(2)该班学生中考体育成绩的中位数落在 组;(在A、B、C、D、E中选出正确答案填在横线上)
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.