题目内容
【题目】如图,△ABC是等边三角形,D是三角形外一动点,满足∠ADB=600,
(1)当D点在AC的垂直平分线上时,求证: DA+DC=DB.
(2)当D点不在AC的垂直平分线上时,(1)中的结论是否仍然成立?请说明理由.
(3)当D点在如图的位置时,直接写出DA,DC,DB的数量关系,不必证明.
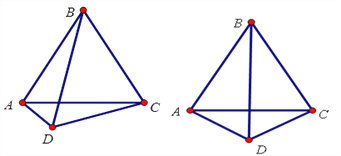
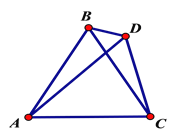
【答案】(1)证明见解析;(2)DA+DC=DB结论成立,证明见解析;(3)DA=DB+DC.
【解析】试题分析:(1)由D点在AC的垂直平分线上,可得AD=CD,又由∠ADB=60°,△ABC是等边三角形,可得△ABD是含30°角的直角三角形,继而证得结论;
(2)首先在DB上截取DE=AD,可证得△ADE是等边三角形,又由△ABC是等边三角形,易证得△BAE≌△CAD(SAS),继而证得结论.
(3)DA=DB+DC.
试题解析:证明:(1)∵D点在AC的垂直平分线上,
∴AD=CD,
∴∠DAC=∠DCA,∠ADB=∠CDB=60°,
∴∠DAC=30°,
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠BAD=90°,
∴∠ABD=90°-∠ADB=30°,
∴BD=2AD=AD+CD;
(2)成立.
理由:在DB上截取DE=AD,
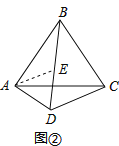
∵∠ADB=60°,
∴△ADE是等边三角形,
∴AE=AD,∠EAD=60°,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠BAE=∠CAD,
在△BAE和△CAD中,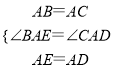 ,
,
∴△BAE≌△CAD(SAS),
∴BE=CD,
∴BD=DE+BE=AD+CD.
(3)DA=DB+DC.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目