题目内容
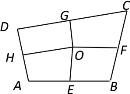
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E,G,H,F分别在AB,BC,CD,AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE,PF,PG,PH,则△PEF和△PGH的面积和等于 . 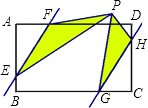
【答案】7
【解析】∵在矩形ABCD中,AD=6,AB=4,AF=CG=2,BE=DH=1,
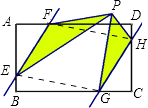
∴AE=AB﹣BE=4﹣1=3,
CH=CD﹣DH=4﹣1=3,
∴AE=CH,
在△AEF与△CGH中, 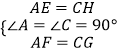 ,
,
∴△AEF≌△CGH(SAS),
∴EF=GH,
同理可得,△BGE≌△DFH,
∴EG=FH,
∴四边形EGHF是平行四边形,
∵△PEF和△PGH的高的和等于点H到直线EF的距离,
∴△PEF和△PGH的面积和= ![]() ×平行四边形EGHF的面积,
×平行四边形EGHF的面积,
∵平行四边形EGHF的面积
=4×6﹣ ![]() ×2×3﹣
×2×3﹣ ![]() ×1×(6﹣2)﹣
×1×(6﹣2)﹣ ![]() ×2×3﹣
×2×3﹣ ![]() ×1×(6﹣2),
×1×(6﹣2),
=24﹣3﹣2﹣3﹣2,
=14,
∴△PEF和△PGH的面积和= ![]() ×14=7.
×14=7.
故答案为:7.
由矩形性质得AD=6,AB=4,AF=CG=2,BE=DH=1,从而得出AE=CH;根据全等三角形的判定SAS可得△AEF≌△CGH,依据全等三角形的性质可得EF=GH;同理可得:△BGE≌△DFH,EG=FH,两组对边分别相等的四边形是平行四边形,由此得四边形EGHF是平行四边形,从而得出S△PEF+S△PGH=![]() S平行四边形EGHF,求出平行四边形EGHF的面积,即可得那两个三角形面积之和.
S平行四边形EGHF,求出平行四边形EGHF的面积,即可得那两个三角形面积之和.

 特高级教师点拨系列答案
特高级教师点拨系列答案【题目】某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔.每位女生的身高统计如图,部分统计量如表:
平均数 | 标准差 | 中位数 | |
甲队 | 1.72 | 0.038 | |
乙队 | 0.025 | 1.70 |
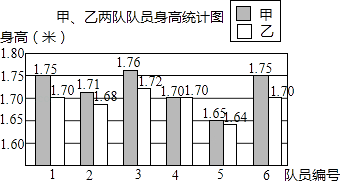
(1)求甲队身高的中位数;
(2)求乙队身高的平均数及身高不小于1.70米的频率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队中哪一队将被录取?请说明理由.