Question

7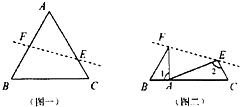． 如图一，将等边三角形ABC沿直线EF对折（图一），使A点落在BC上（图二），请问图二中1，2所标示的两个角的度数之差为多少度？答案：0度．

Answer 1

分析 三角形ABC是等边三角形，所以∠A=∠B=∠C=60°，因为三角形的内角和是180°，所以在三角形EAC中：∠2+∠EAC=180°-60°=120°，因为∠A=60°，所以∠1+∠EAC=180°-60°=120°，所以∠1=∠2，由此即可得出结论．

解答 解：三角形ABC是等边三角形，所以∠A=∠B=∠C=60°，
因为三角形的内角和是180°，所以在三角形EAC中：∠2+∠EAC=180°-60°=120°，
因为∠A=60°，所以∠1+∠EAC=180°-60°=120°，所以∠1=∠2，
所以∠1-∠2=0°；
故答案为：0．

点评 此题属于简单图形的折叠问题，推出：∠2+∠EAC=∠1+∠EAC=120°，是解答此题的关键．