[例1](2006天津)某射手进行射击训练,假设每次射击击中目标的概率为 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。
(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);
(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);
(3)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.
解(Ⅰ):记“射手射击1次,击中目标”为事件 ,则在3次射击中至少有两次连续击中目标的概率
,则在3次射击中至少有两次连续击中目标的概率


(Ⅱ)解:射手第3次击中目标时,恰好射击了4次的概率

(Ⅲ)解:由题设,“ξ=k”的概率为

 (
( 且
且 )
)
所以,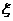 的分布列为:
的分布列为:
|
ξ |
3 |
4 |
… |
k |
… |
|
P |
 |
 |
… |
 |
… |
[例2](2004春安微)已知盒中有10个灯泡,其中8个正品,2个次品。需要从中取出2个正品,每次从中取出1个,取出后不放回,直到取出2个正品为止,设ξ为取出的次数,求ξ的分布列及Eξ。
解: ;
;
 ;
;
 。
。
ξ的分布列表略--
E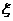 =
= 。
。
◆提炼方法:求分布列的两个关键--
1.确定随机变量的取值;2.计算取每个值的概率.
[例3]盒中装有一打(12个)乒乓球,其中9个新的,3个旧的(用过的球即为旧的),从盒中任取3个使用,用完后装回盒中,此时盒中旧球个数ξ是一个随机变量,求ξ的分布列
分析:从盒中任取3个,这3个可能全是旧的,2个旧的1个新的,1个旧的2个新的或全是新的,所以用完放回盒中,盒中旧球个数可能是3个,4个,5个,6个,即ξ可以取3,4,5,6
解:ξ的所有可能取值为3,4,5,6
P(ξ=3)= =
= ;P(ξ=4)=
;P(ξ=4)= =
= ;
;
P(ξ=5)= =
= ;P(ξ=6)=
;P(ξ=6)= =
=
ξ的分布列表略--
[例4]某人骑车从家到学校的途中有5个路口,假设他在各个路口遇到红灯的事件是相互独立的,且概率均为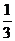 .(1)求此人在途中遇到红灯的次数
.(1)求此人在途中遇到红灯的次数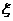 的分布列; (2)求此人首次遇到红灯或到达目的地而停车时所经过的路口数
的分布列; (2)求此人首次遇到红灯或到达目的地而停车时所经过的路口数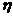 的分布列; (3)此人途中至少遇到一次红灯的概率.
的分布列; (3)此人途中至少遇到一次红灯的概率.
解:(1)由已知 ,故分布列
,故分布列 ,
, .
.
(2)η=k(k=0,1,2,3,4)表示事件:前k个路口均为绿灯,第k+1个路口为红灯;
η=5表示5个路口均为绿灯.故所求的分布列为: ,
,  .
.
(3)
◆提炼方法:要能从所给的条件中看出特殊的分布,如本题中 .
.
[研讨.欣赏]某人参加射击,击中目标的概率是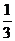
①设ξ为他射击6次击中目标的次数,求随机变量ξ的分布列;
②设η为他第一次击中目标时所需要射击的次数,求η的分布列;
③若他连续射击6次,设ξ为他第一次击中目标的次数,求ξ的分布列;
④若他只有6颗子弹,若他击中目标,则不再射击,否则子弹打完,求他
射击次数ξ的分布列
解:①随机变量ξ服从二项分布 ,而ξ的取值为0,1,2,3,4,5,6,则
,而ξ的取值为0,1,2,3,4,5,6,则
故ξ的分布列为:
|
ξ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
P |
 |
 |
 |
 |
 |
 |
 |
②设 表示他前
表示他前 次未击中目标,而在第
次未击中目标,而在第 次射击时击中目标,则
次射击时击中目标,则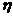 的取值为全体正整数1,2,3,… 则
的取值为全体正整数1,2,3,… 则
∴η的分布列为
|
η |
1 |
2 |
3 |
4 |
… |
k |
… |
|
P |
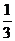 |
 |
 |
 |
… |
 |
… |
③设ξ=k+1表示前k次未击中目标,而第k+1次击中目标,ξ的取值为0,1,2,3,4,5,当ξ=6时,表示射击6次均未击中目标
则 而
而
 的分布列为
的分布列为
|
ξ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
P |
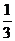 |
 |
 |
 |
 |
 |
 |
④设 ,表示前
,表示前 次未击中,而第
次未击中,而第 次击中,
次击中,
 ;
;
而 表示前5次未击中,第6次可以击中,也可以未击中
表示前5次未击中,第6次可以击中,也可以未击中
 ,
, 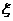 的分布列为:
的分布列为:
|
ξ |
1 |
2 |
3 |
4 |
5 |
6 |
|
P |
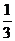 |
 |
 |
 |
 |
 |
 B.
B. C.110
D.55
C.110
D.55 3),ξ的分布列是P(ξ=k)=C
3),ξ的分布列是P(ξ=k)=C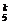 0
0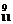 ·(
·(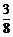 )9(
)9(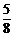 )2×
)2× p0·(1-p)2=
p0·(1-p)2= ,
,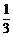 ,P(η≥1)=1-P(η=0)=1-C
,P(η≥1)=1-P(η=0)=1-C (
(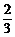 )4=1-
)4=1- =
= 答
答