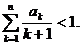5.几何分布:如:某射击手击中目标的概率为p,则从射击开始到击中目标所需次数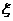 的分布列为
的分布列为
|
ξ |
1 |
2 |
3 |
… |
k |
… |
|
P |
p |
qp |
q2p |
… |
qk-1p |
… |
这种种分布列叫几何分布,记作g(k,p)= qk-1p,其中k=0,1,2,…,q=1-p.
4. 二项分布:在n次独立重复试验中,事件A发生的次数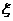 是一个随机变量,其所有可能取的值为0,1,2,3,…,n,并且P(ξ=k)=Cnkpkqn-k(其中k=0,1,2,…,n,p+q=1),即分布列为
是一个随机变量,其所有可能取的值为0,1,2,3,…,n,并且P(ξ=k)=Cnkpkqn-k(其中k=0,1,2,…,n,p+q=1),即分布列为
|
ξ |
0 |
1 |
… |
k |
… |
n |
|
P |
Cn0p0qn |
Cn1p1qn-1 |
… |
Cnkpkqn-k |
… |
Cnnpnq0 |
称这样的随机变量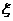 服从参数为n和p的二项分布,记作:
服从参数为n和p的二项分布,记作: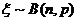 .
.
3. 离散型随机变量的分布列:
设离散型随机变量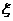 可能取的值为x1,x2,……xi…,且P(ξ=xi)=pi,则称
可能取的值为x1,x2,……xi…,且P(ξ=xi)=pi,则称
|
ξ |
x1 |
x2 |
… |
xi |
… |
|
p |
p1 |
p2 |
… |
pi |
… |
为随机变量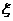 的分布列。
的分布列。
(1)离散型随机变量的分布列的两个性质:
①P(ξ=xi)=pi≥0;②p1+p2+……=1
(2)求分布列的方法步骤:
①确定随机变量的所有取值; ②计算每个取值的概率并列表。
5. 某地为了防止水土流失,植树造林,绿化荒沙地,每年比上一年多植相同亩数的林木,但由于自然环境和人为因素的影响,每年都有相同亩数的土地沙化,具体情况为下表所示:
|
|
1998年 |
1999年 |
2000年 |
|
新植亩数 |
1000 |
1400 |
1800 |
|
沙地亩数 |
25200 |
24000 |
22400 |
而一旦植完,则不会被沙化.
问:(1)每年沙化的亩数为多少?
(2)到那一年可绿化完全部荒沙地?
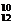 (
(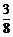 )10·(
)10·(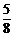 )2 B.C
)2 B.C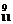 (
(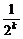 ,k=1,2,…,则P(2<ξ≤4)等于
,k=1,2,…,则P(2<ξ≤4)等于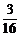 B.
B.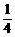 C.
C.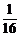 D.
D.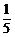
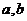 是常数,则η也是随机变量.如出租车里程与收费.
是常数,则η也是随机变量.如出租车里程与收费.
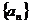 满足
满足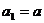 (
(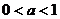 ),且
),且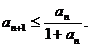 求证
求证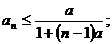 (2)
(2)