10.甲乙两名篮球队员独立地轮流投篮,直到某人投中为止。甲投中的概率为0.4,乙为0.6,分别求出甲乙两人投篮次数的分布列。(假设甲先投)
解:设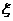 为甲投篮的次数,
为甲投篮的次数,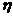 为乙投篮的次数,
为乙投篮的次数,
(1)设事件A=前k-1次均不中,第k次甲中;B=前k-1次均不中,第k次甲不中而乙投中,则A与B互斥,故有: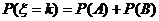
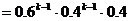
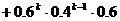
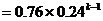 (
(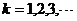 )
)
(2)设事件B=前k-1次均不中,第k次甲不中而乙投中,C=前k次均不中,第k+1次甲投中,则B与C互斥,故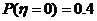 ,
, 
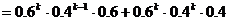
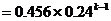 (
(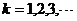 )
)
[探索题]A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员是B1、B2、B3,按以往多次比赛的统计,对阵队员之间胜负概率如下:
|
对阵队员 |
A队员胜的概率 |
A队员负的概率 |
|
A1对B1 |
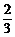 |
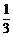 |
|
A2对B2 |
 |
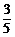 |
|
A3对B3 |
 |
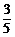 |
现按表中对阵方式出场,每场胜队得1分,负队得0分.设A队、B队最后所得总分分别为ξ、η
(1)求ξ、η的概率分布;
(2)求Eξ、Eη
解:(1)ξ、η的可能取值分别为3,2,1,0
P(ξ=3)=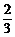 ×
× ×
× =
= ,
,
P(ξ=2)=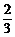 ×
× ×
×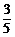 +
+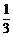 ×
× ×
× +
+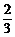 ×
×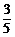 ×
× =
=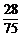 ,
,
P(ξ=1)=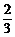 ×
×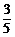 ×
×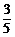 +
+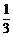 ×
× ×
×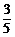 +
+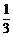 ×
×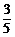 ×
× =
= ,
,
P(ξ=0)=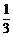 ×
×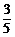 ×
×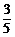 =
=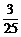 ;
;
根据题意知ξ+η=3,所以
P(η=0)=P(ξ=3)= ,P(η=1)=P(ξ=2)=
,P(η=1)=P(ξ=2)=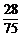 ,
,
P(η=2)=P(ξ=1)= ,P(η=3)=P(ξ=0)=
,P(η=3)=P(ξ=0)=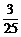
(2)Eξ=3× +2×
+2×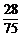 +1×
+1× +0×
+0×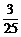 =
=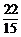 ;
;
因为ξ+η=3,所以Eη=3-Eξ=
7.(2006广东) 某运动员射击一次所得环数x的分布列如下:
|
x |
0-6 |
7 |
8 |
9 |
10 |
|
p |
0 |
0. 2 |
0. 3 |
0. 3 |
0. 2 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为ξ
(Ⅰ)求该运动员两次都命中7环的概率;
(Ⅱ)求ξ分布列;
(Ⅲ) 求ξ的数学希望
解:(Ⅰ)求该运动员两次都命中7环的概率为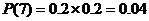 ;
;
(Ⅱ) ξ的可能取值为7, 8 ,9 , 10
ξ的可能取值为7, 8 ,9 , 10
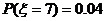
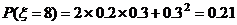
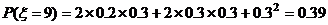
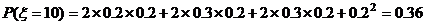
ξ分布列为
|
ξ |
7 |
8 |
9 |
10 |
|
P |
0 04 04 |
0 21 21 |
0 39 39 |
0 36 36 |
(Ⅲ) 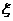 的数学希望为
的数学希望为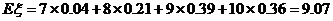
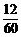 =
=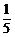 从而P(ξ=k)=C
从而P(ξ=k)=C (
(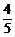 )10-k,k=0,1,2,…,10
)10-k,k=0,1,2,…,10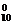 (
(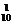 ·
·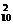 (
(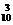 (
( (
(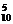 (
( ,即该顾客中奖的概率为
,即该顾客中奖的概率为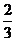 .
.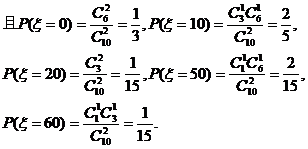
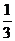

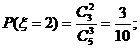
 +
+ =
=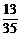 .
.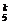 0.3k0.75-k,k=0,1,…,5
0.3k0.75-k,k=0,1,…,5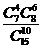 的是 ( )
的是 ( )