21.(本小题满分12分)
已知函数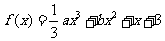 ,其中
,其中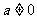


(1) 当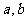 满足什么条件时,
满足什么条件时,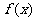 取得极值?
取得极值?
(2) 已知 ,且
,且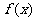 在区间
在区间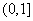 上单调递增,试用
上单调递增,试用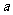 表示出
表示出 的取值范围.
的取值范围.
解: (1)由已知得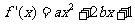 ,令
,令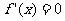 ,得
,得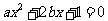 ,
,
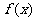 要取得极值,方程
要取得极值,方程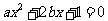 必须有解,
必须有解,
所以△ ,即
,即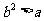 , 此时方程
, 此时方程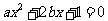 的根为
的根为
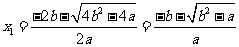 ,
,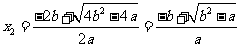 ,
,
所以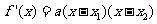


当 时,
时,
|
x |
(-∞,x1) |
x 1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
f’(x) |
+ |
0 |
- |
0 |
+ |
|
f (x) |
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
所以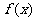 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
当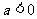 时,
时, 

|
x |
(-∞,x2) |
x 2 |
(x2,x1) |
x1 |
(x1,+∞) |
|
f’(x) |
- |
0 |
+ |
0 |
- |
|
f (x) |
减函数 |
极小值 |
增函数 |
极大值 |
减函数 |
所以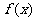 在x 1, x2处分别取得极大值和极小值.
在x 1, x2处分别取得极大值和极小值.
综上,当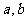 满足
满足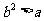 时,
时, 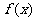 取得极值.
取得极值. 

(2)要使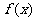 在区间
在区间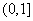 上单调递增,需使
上单调递增,需使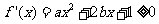 在
在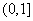 上恒成立.
上恒成立.
即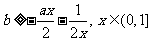 恒成立, 所以
恒成立, 所以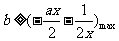
设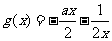 ,
,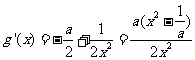 ,
,
令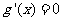 得
得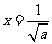 或
或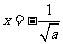 (舍去),
(舍去), 

当 时,
时,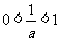 ,当
,当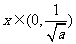 时
时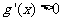 ,
,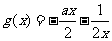 单调增函数;
单调增函数;
当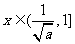 时
时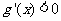 ,
,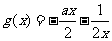 单调减函数,
单调减函数,
所以当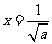 时,
时,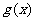 取得最大,最大值为
取得最大,最大值为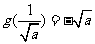 .
.
所以
当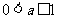 时,
时,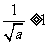 ,此时
,此时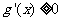 在区间
在区间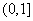 恒成立,所以
恒成立,所以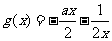 在区间
在区间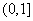 上单调递增,当
上单调递增,当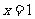 时
时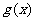 最大,最大值为
最大,最大值为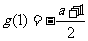 ,所以
,所以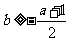
综上,当 时,
时,  ; 当
; 当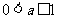 时,
时, 


[命题立意]:本题为三次函数,利用求导的方法研究函数的极值、单调性和函数的最值,函数在区间上为单调函数,则导函数在该区间上的符号确定,从而转为不等式恒成立,再转为函数研究最值.运用函数与方程的思想,化归思想和分类讨论的思想解答问题.
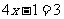 的解是( )B
的解是( )B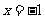 B.
B.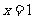 C.
C.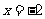 D.
D.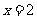
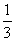 xa+2y3与-3x3y2b-1是同类项,那么a、b的值分别是( )A
xa+2y3与-3x3y2b-1是同类项,那么a、b的值分别是( )A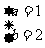 B.
B.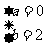 C.
C.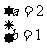 D.
D.
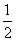 B.
B. 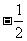 C. 2
D.-2
C. 2
D.-2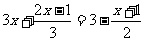 去分母正确的是( ) A
去分母正确的是( ) A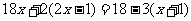 B.
B.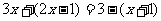 C.
C.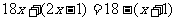 D.
D.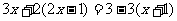
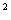 +y
+y
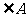 、
、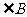 互余,
互余,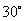 .设
.设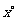 、
、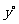 ,下列方程组中符合题意的是( )C
,下列方程组中符合题意的是( )C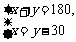 B.
B. 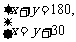 C.
C.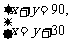 D.
D.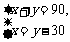
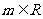 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量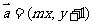 ,向量
,向量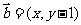 ,
,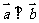 ,动点
,动点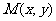 的轨迹为E.
的轨迹为E.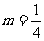 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且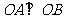 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;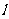 与圆C:
与圆C: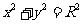 (1<R<2)相切于A1,且
(1<R<2)相切于A1,且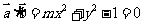 , 即
, 即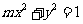 .
.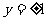 ;
;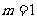 时, 方程表示的是圆
时, 方程表示的是圆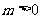 且
且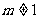 时,方程表示的是椭圆;
时,方程表示的是椭圆; 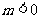 时,方程表示的是双曲线.
时,方程表示的是双曲线.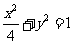 ,设圆心在原点的圆的一条切线为
,设圆心在原点的圆的一条切线为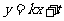 ,解方程组
,解方程组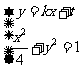 得
得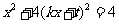 ,即
,即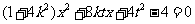 ,
,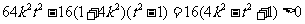 ,
,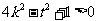 ,即
,即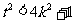 ,
且
,
且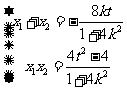
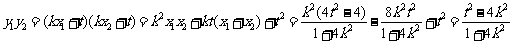 ,
,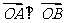 , 需使
, 需使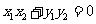 ,即
,即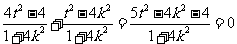 ,
,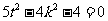 , 即
, 即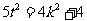 且
且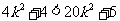 恒成立.
恒成立.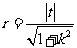 ,
,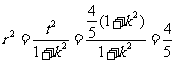 , 所求的圆为
, 所求的圆为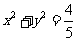 .
.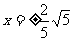 ,与
,与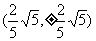 或
或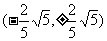 也满足
也满足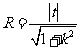 , 即
, 即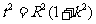 ①,
①,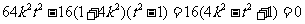 , 即
, 即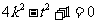 ,
②
,
②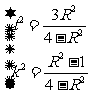 , 此时A,B重合为B1(x1,y1)点,
, 此时A,B重合为B1(x1,y1)点,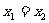 ,所以,
,所以,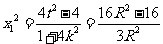 ,
, 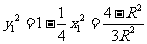 ,所以
,所以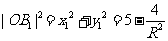 ,
,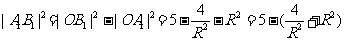 因为
因为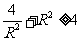 当且仅当
当且仅当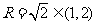 时取等号,所以
时取等号,所以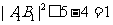 ,即
,即