5.(天津市天津一中2010届高三第四次月考理科)设三条不同的直线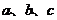 ,两个不同的平面
,两个不同的平面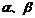 ,
,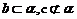 。则下列命题不成立的是( B )
。则下列命题不成立的是( B )
A.若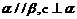 ,则
,则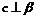 B.“若
B.“若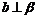 ,则
,则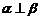 ”的逆命题
”的逆命题
C.若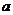 是
是 在
在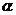 的射影,
的射影,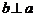 则
则 D.“若
D.“若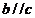 ,则
,则 ”的逆否命题
”的逆否命题
5.(天津市天津一中2010届高三第四次月考理科)设三条不同的直线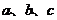 ,两个不同的平面
,两个不同的平面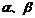 ,
,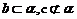 。则下列命题不成立的是( B )
。则下列命题不成立的是( B )
A.若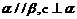 ,则
,则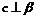 B.“若
B.“若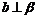 ,则
,则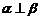 ”的逆命题
”的逆命题
C.若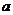 是
是 在
在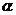 的射影,
的射影,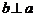 则
则 D.“若
D.“若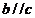 ,则
,则 ”的逆否命题
”的逆否命题