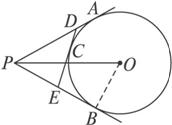
摘要：解:如图5-21建立空间直角坐标系 由题意.有A.C.E 设D点的坐标为(0.0.z)(z>0) 则={1.1.0}.={0.-2.z}. 设与所成角为θ. 则·=·cosθ=-2.且AD与BE所成的角的大小为arccos.∴cos2θ=.∴z=4.故|BD|的长度为4. 又VA-BCD=|AB|×|BC|×|BD|=.因此.四面体ABCD的体积为. 评述:本题考查空间图形的长度.角度.体积的概念和计算.以向量为工具.利用空间向量的坐标表示.空间向量的数量积计算线段的长度.异面直线所成角等问题.思路自然.解法灵活简便.
网址：http://m.1010jiajiao.com/timu_id_4435243[举报]
| |||||||||||
，
，(G为动点，P是HP和GF的交点)
的轨迹方程；
、
，且线段
的中垂线与
，则
＜
(
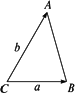
为已知△ABC中，a＝5，b＝8，
＝－20，试求C．
有个同学求解如下：
解：如图，∵
＝b＝8，
∴cos∠C＝
．
又∵0°≤∠C≤180°，
∴∠C＝120°．
这位同学的解答正确吗？如果你是他的数学老师，你会给他写什么批语？
如图，某隧道设计为双向四车道，车道总宽22米，要求通行车辆限高4.5米，隧道全长2.5千米，隧道的拱线近似地看成半个椭圆形状．
(Ⅰ)若最大拱高h为6米，则隧道设计的拱宽l是多少？
(Ⅱ)若最大拱高h不小于6米，则应如何设计拱高h和拱宽l，才能使半个椭圆形隧道的土方工程量最小？
(半个椭圆的面积公式为S＝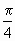
lh，柱体体积为：底面积乘以高．本题结果均精确到0.1米)
| |||||||||||
，|BC|＝2|AC|．
．