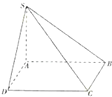（2011•许昌三模）已知四棱锥S-ABCD中，AB=BC=CD=DA=SA=2，底面ABCD是正方形，SD=SB=2

2

．
（I）在该四棱锥中，是否存在一条侧棱垂直于底面？如果存在，请给出证明；
（Ⅱ）用多少个这样的四棱锥可以拼成一个棱长为2的正方体ABCD-A₁B₁C₁D₁？说明你的结论．
（Ⅲ）在（Ⅱ）的条件下，设正方体ABCD-A₁B₁C₁D₁的棱BB₁的中点为N，棱DD₁的中点为M，求二面角A-MN-C的大小的余弦值．

（2012•浦东新区一模）动点P在边长为1的正方体ABCD-A₁B₁C₁D₁的对角线BD₁上从B向D₁移动，点P作垂直于面BB₁D₁D的直线与正方体表面交于M，N，BP=x，MN=y，则函数y=f（x）的解析式为．

如图，正方体ABCD-A₁B₁C₁D₁的棱长为1，线段B₁D₁上有两个动点E，F，且EF=

2

2

，则下列结论中错误的个数是（　　） 
（1）AC⊥BE．
（2）若P为AA₁上的一点，则P到平面BEF的距离为

2

2

．
（3）三棱锥A-BEF的体积为定值．
（4）在空间与DD₁，AC，B₁C₁都相交的直线有无数条．
（5）过CC₁的中点与直线AC₁所成角为40°并且与平面BEF所成角为50°的直线有2条．

（2013•湖州二模）正方体ABCD-A₁B₁C₁D₁的棱长为2，MN是它的内切球的一条弦（把球面上任意两点之间的线段称为球的弦），P为正方体表面上的动点，当弦MN最长时.

PM

•

PN

的最大值为．

在正方体ABCD-A₁B₁C₁D₁中，有下面结论：
①AC∥平面CB₁D₁；
②AC₁⊥平面CB₁D₁；
③AC₁与底面ABCD所成角的正切值是

2

2

；
④AD₁与BD为异面直线．
其中正确的结论的序号是．（把你认为正确的结论的序号都填上）