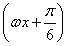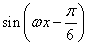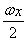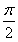摘要：已知函数f(x)=sin(x+)+sin(x-)-2cos2,x∈R(其中＞0). 的值域, (2)若对任意的a∈R.函数y=f(x),x∈(a,a+］的图象与直线y=-1有且仅有两个不同的交点.试确定的值.并求函数y=f(x),x∈R的单调增区间. 解 = =2-1 =2sin -1. 由-1≤sin≤1,得-3≤2sin-1≤1. 可知函数f(x)的值域为［-3.1］. (2)由题设条件及三角函数图象和性质可知.y=f(x)的周期为,又由＞0,得=,即得=2. 于是有f(x)=2sin-1, 再由2k-≤2x-≤2k+. 解得k-≤x≤k+. 所以y=f(x)的单调增区间为.
网址：http://m.1010jiajiao.com/timu_id_4020068[举报]
已知函数f(x)=sin(ωx+
)+sin(ωx-
)-2cos2
，x∈R（其中ω＞0）
（I）求函数f（x）的值域；
（II）若函数y=f（x）的图象与直线y=-1的两个相邻交点间的距离为
，求函数y=f（x）的单调增区间．
查看习题详情和答案>>
| π |
| 6 |
| π |
| 6 |
| ωx |
| 2 |
（I）求函数f（x）的值域；
（II）若函数y=f（x）的图象与直线y=-1的两个相邻交点间的距离为
| π |
| 2 |
已知函数f(x)=sin(ωx+
)+sin(ωx-
)-2cos2
，x∈R（其中ω＞0）
（I）求函数f（x）的值域；
（II）若函数y=f（x）的图象与直线y=-1的两个相邻交点间的距离为
，求函数y=f（x）的单调增区间．
查看习题详情和答案>>
| π |
| 6 |
| π |
| 6 |
| ωx |
| 2 |
（I）求函数f（x）的值域；
（II）若函数y=f（x）的图象与直线y=-1的两个相邻交点间的距离为
| π |
| 2 |
已知函数f(x)＝sin
＋sin
－2cos2
，x∈R，其中
＞0．
(1)求函数f(x)的值域；
(2)若对任意的a∈R，函数y＝f(x)，x∈(a，a＋π]的图象与直线y＝－1有且仅有两个不同的交点，试确定
的值(不必证明)，并求函数y＝f(x)的单调增区间．
＋
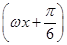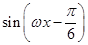－2cos2
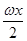，x∈R(其中ω＞0)．
，求函数y＝f(x)的单调增区间．
