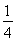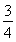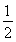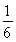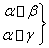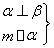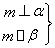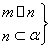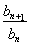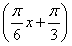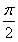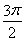题目内容
已知函数f(x)＝sin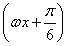
＋
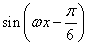－2cos2
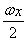，x∈R(其中ω＞0)．
(1)求函数f(x)的值域；
(2)若函数y＝f(x)的图象与直线y＝－1的两个相邻交点间的距离为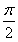
，求函数y＝f(x)的单调增区间．
（1）[－3,1]（2）
(k∈Z)
【解析】(1)f(x)＝
sin ωx＋
cos ωx＋
sin ωx－
cos ωx－(cos ωx＋1)
＝2
－1＝2
－1.
由－1≤≤1，得－3≤2s－1≤1，
所以函数f(x)的值域为[－3,1]．
(2)由题设条件及三角函数图象和性质可知，y＝f(x)的周期为π，所以
＝π，即ω＝2.
所以f(x)＝2sin
－1，
再由2kπ－
≤2x－
≤2kπ＋
(k∈Z)，解得kπ－
≤x≤kπ＋
(k∈Z)．
所以函数y＝f(x)的单调增区间为
(k∈Z)．
练习册系列答案
状元坊全程突破导练测系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
