摘要：面面成角 方法一:直接作二面角 方法二:面积法 PC ┴ 面ABC.记二面角P-AB-C为θ.则 (先写公共边/点.再按垂线依次往后写.垂足放在分子) 附:使用时.可能会正弦定理与余弦定理搭配使用. 正弦定理: 余弦定理: 方法三:向量法 求.β所成二面角x.先求α .法向量 所成的角θ 则 求距离 点到平面的距离 方法一:等体积法(注意点的平移.以及体积的等量代换) 例:求点B到PAC的距离h (注意余弦定理.正弦定理的综合应用) 方法二:向量法 同上.设面PAC的法向量为n .在面PAC上任取一点.不妨碍取P.则 P A B C
网址：http://m.1010jiajiao.com/timu_id_4016821[举报]
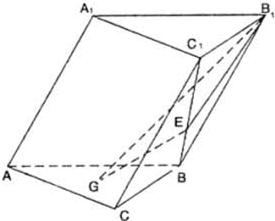如图，斜三棱柱ABC-A1B1C1中，侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成60°的角，AA1=2，低面ABC是边长为2的正三角形，其重心为G点（重心为三条中线的交点）．E是线段BC1上一点且BE=| 1 | 3 |
（1）求证：GE∥侧面AA1B1B；
（2）求平面B1GE与底面ABC所成锐二面角的大小． 查看习题详情和答案>>
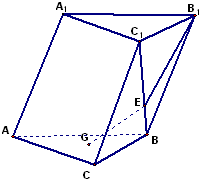如图，在斜三棱柱ABC-A1B1C1中，侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成60°角，AA1=2，底面ABC是边长为2的三角形，G为三角形ABC内一点，E是线段BC1上一点，且| BE |
| 1 |
| 3 |
| BC1 |
| GE |
| 1 |
| 3 |
| AB1 |
（1）请判断点G在三角形ABC内的位置；
（2）求平面B1GE与底面ABC所成锐角二面角的大小．
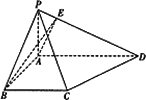
在四棱锥P—ABCD中，底面ABCD是一直角梯形，
，
与底面成30°角。
（1）若
为垂足，求证：
；
（2）在（1）的条件下，求异面直线AE与CD所成角的余弦值；
（3）求平面PAB与平面PCD所成的锐二面角的正切值。
查看习题详情和答案>>
，则
；
；
．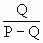