题目内容
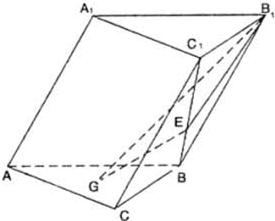 如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2,低面ABC是边长为2的正三角形,其重心为G点(重心为三条中线的交点).E是线段BC1上一点且BE=
如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2,低面ABC是边长为2的正三角形,其重心为G点(重心为三条中线的交点).E是线段BC1上一点且BE=| 1 | 3 |
(1)求证:GE∥侧面AA1B1B;
(2)求平面B1GE与底面ABC所成锐二面角的大小.
分析:(1)欲证GE∥侧面AA1B1B,根据直线与平面平行的判定定理可知只需证GE与侧面AA1B1B 内一直线平行,延长B1E交BC于F,而GE∥AB1,GE?侧面AA1B1B,AB1?侧面AA1B1B,满足定理的条件;
(2)过B1作B1H⊥AB,垂足为H,在底面ABC内,过H作HT⊥AF,垂足为T,连B1T,根据二面角平面角的定义可知∠B1TH为所求二面角的平面角,在Rt△B1HT中求出此角的正切值即可.
(2)过B1作B1H⊥AB,垂足为H,在底面ABC内,过H作HT⊥AF,垂足为T,连B1T,根据二面角平面角的定义可知∠B1TH为所求二面角的平面角,在Rt△B1HT中求出此角的正切值即可.
解答: 解:(1)延长B1E交BC于F,
解:(1)延长B1E交BC于F,
∵△B1EC1∽△FEB,BE=
EC1
∴BF=
B1C1=
BC,从而F为BC的中点. (2分)
∵G为△ABC的重心,
∴A、G、F三点共线,且=
=
=
,
∴GE∥AB1,
又GE?侧面AA1B1B,AB1?侧面AA1B1B,
∴GE∥侧面AA1B1B (4分)
(2)在侧面AA1B1B内,过B1作B1H⊥AB,垂足为H,
∵侧面AA1B1B⊥底面ABC,
∴B1H⊥底面ABC.又侧棱AA1与底面ABC成60°的角,AA1=2,
∴∠B1BH=60°,BH=1,B1H=
(6分)
在底面ABC内,过H作HT⊥AF,垂足为T,连B1T.由三垂线定理有B1T⊥AF,又平面B1GE与底面ABC的交线为AF,
∴∠B1TH为所求二面角的平面角(8分)
∴AH=AB+BH=3,∠HAT=30°,
∴HT=AHsin30°=
,
在Rt△B1HT中,tan∠B1TH=
=
(10分)
从而平面B1GE与底面ABC所成锐二面角的大小为arctan
(12分)
 解:(1)延长B1E交BC于F,
解:(1)延长B1E交BC于F,∵△B1EC1∽△FEB,BE=
| 1 |
| 2 |
∴BF=
| 1 |
| 2 |
| 1 |
| 2 |
∵G为△ABC的重心,
∴A、G、F三点共线,且=
| FG |
| FA |
| FE |
| FB1 |
| 1 |
| 3 |
∴GE∥AB1,
又GE?侧面AA1B1B,AB1?侧面AA1B1B,
∴GE∥侧面AA1B1B (4分)
(2)在侧面AA1B1B内,过B1作B1H⊥AB,垂足为H,
∵侧面AA1B1B⊥底面ABC,
∴B1H⊥底面ABC.又侧棱AA1与底面ABC成60°的角,AA1=2,
∴∠B1BH=60°,BH=1,B1H=
| 3 |
在底面ABC内,过H作HT⊥AF,垂足为T,连B1T.由三垂线定理有B1T⊥AF,又平面B1GE与底面ABC的交线为AF,
∴∠B1TH为所求二面角的平面角(8分)
∴AH=AB+BH=3,∠HAT=30°,
∴HT=AHsin30°=
| 3 |
| 2 |
在Rt△B1HT中,tan∠B1TH=
| B1H |
| HT |
2
| ||
| 3 |
从而平面B1GE与底面ABC所成锐二面角的大小为arctan
2
| ||
| 3 |
点评:本题主要考查了直线与平面平行的判定,以及二面角的度量等基础知识,考查空间想象能力,运算能力和推理论证能力,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
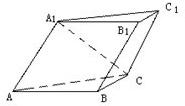 已知如图,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
已知如图,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2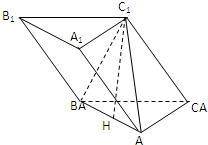 如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.
如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.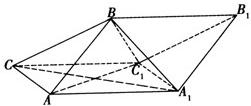 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点. (2012•潍坊二模)如图,斜三棱柱ABC-A1B1C1,侧面BB1C1C⊥底面ABC,△BC1C是等边三角形,AC⊥BC,AC=BC=4.
(2012•潍坊二模)如图,斜三棱柱ABC-A1B1C1,侧面BB1C1C⊥底面ABC,△BC1C是等边三角形,AC⊥BC,AC=BC=4.