题目内容
在四棱锥P－ABCD中，底面ABCD是一直角梯形，∠BAD＝90°，AD∥BC，AB＝BC＝a，AD＝2a，PA⊥底面ABCD，PD与底面成30°角．
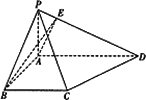
(1)若AE⊥PD，E为垂足，求证：BE⊥PD；
(2)在(1)的条件下，求异面直线AE与CD所成角的余弦值；
(3)求平面PAB与平面PCD所成的锐二面角的正切值．
答案：
解析：
解析：
|
解法：(1)如图建立空间直角坐标系，
(2)由(1)知， |
4分
练习册系列答案
相关题目
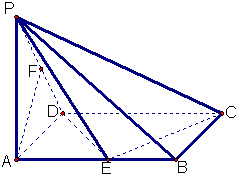已知在四棱锥P一ABCD中，底面ABCD是矩形，PA⊥平面ABCD，
如图．在四棱锥P一ABCD中，底面ABCD是正方形，侧棱PD⊥底 面ABCD，PD=DC=2，E是PC的中点．
已知在四棱锥P一ABCD中，二面角P一AD一B为60°，∠PDA=45°，∠DAB=90°，∠PAD=90°，∠ADC=135°，
如图，在四棱锥P一ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．PA=PD=AD=2，点M在线段PC上 PM=
（本小题满分14分）在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD与底面ABCD垂直，PD=DC，E是PC的中点，作EF
于点F（Ⅰ）证明PA
平面EBD．
平面EFD．
的余弦值；