摘要:圆的方程: ⑴圆的标准方程:. ⑵圆的一般方程:.特别提醒:只有当时.方程才表示圆心为.半径为的圆(二元二次方程表示圆的充要条件是什么? (且且)), ⑶圆的参数方程:(为参数).其中圆心为.半径为.圆的参数方程的主要应用是三角换元:, . ⑷为直径端点的圆方程 如(1)圆C与圆关于直线对称.则圆C的方程为 (答:),(2)圆心在直线上.且与两坐标轴均相切的圆的标准方程是 (答:或),(3)已知是圆(为参数.上的点.则圆的普通方程为 .P点对应的值为 .过P点的圆的切线方程是 (答:,,),(4)如果直线将圆:x2+y2-2x-4y=0平分.且不过第四象限.那么的斜率的取值范围是 方程x2+y2-x+y+k=0表示一个圆.则实数k的取值范围为 (答:),(6)若(为参数...若.则b的取值范围是 (答:)
网址:http://m.1010jiajiao.com/timu_id_4009531[举报]
椭圆 的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线
的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线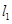 过点
过点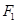 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线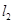 垂直
垂直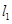 于点
于点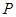 ,线段
,线段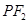 垂直平分线交
垂直平分线交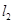 于点
于点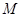
(1)求椭圆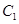 的标准方程和动点
的标准方程和动点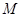 的轨迹
的轨迹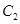 的方程。
的方程。
(2)过椭圆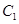 的右焦点
的右焦点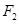 作斜率为1的直线交椭圆于A、B两点,求
作斜率为1的直线交椭圆于A、B两点,求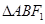 的面积。
的面积。
(3)设轨迹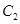 与
与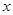 轴交于点
轴交于点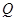 ,不同的两点
,不同的两点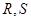 在轨迹
在轨迹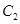 上,
上,
满足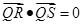 求证:直线
求证:直线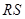 恒过
恒过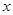 轴上的定点。
轴上的定点。
查看习题详情和答案>>
 , 求椭圆的标准方程;
, 求椭圆的标准方程; ,它的一个焦点是
,它的一个焦点是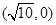 ,求双曲线的标准方程。
,求双曲线的标准方程。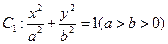 的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线
的长轴长为4,焦距为2,F1、F2分别为椭圆的左、右焦点,直线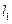 过点
过点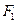 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线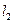 垂直
垂直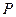 ,线段
,线段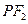 垂直平分线交
垂直平分线交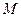
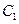 的标准方程和动点
的标准方程和动点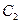 的方程。
的方程。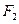 作斜率为1的直线交椭圆于A、B两点,求
作斜率为1的直线交椭圆于A、B两点,求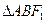 的面积。
的面积。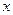 轴交于点
轴交于点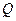 ,不同的两点
,不同的两点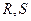 在轨迹
在轨迹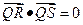 求证:直线
求证:直线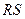 恒过
恒过