摘要：xn-yn(n∈N*)能被x-y整除. 提示:(1)n=1时.x1-y1能被x-y整除. (2)假设当n=k(k≥1)时命题成立.即xk-yk能被x-y整除. 那么n=k+1时. xk+1-yk+1=x·xk-y·yk=x(xk-yk)+x·yk-y·yk=x(xk-yk)+yk(x-y). 由归纳假设xk-yk及x-y能被x-y整除.所以xk+1-yk+1能被x-y整除.
网址：http://m.1010jiajiao.com/timu_id_3981658[举报]
| |||||||||||||||
，证明：当n＞3时，Sn＞3．
已知数列{xn}，{yn}满足x1=x2=1，y1=y2=2，并且
=λ
，
≥λ
（λ为非零参数，n=2，3，4，…）．
（1）若x1，x3，x5成等比数列，求参数λ的值；
（2）当λ＞0时，证明
≤
(n∈N*)；当λ＞1时，证明：
+
+…+
＜
(n∈N*)．
查看习题详情和答案>>
| xn+1 |
| xn |
| xn |
| xn-1 |
| yn+1 |
| yn |
| yn |
| yn-1 |
（1）若x1，x3，x5成等比数列，求参数λ的值；
（2）当λ＞0时，证明
| xn+1 |
| yn+1 |
| xn |
| yn |
| x1-y1 |
| x2-y2 |
| x2-y2 |
| x3-y3 |
| xn-yn |
| xn+1-yn+1 |
| λ |
| λ-1 |
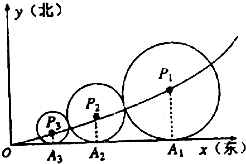为建设好长、株、潭“两型社会”改革实验区，加快二市经济一体化进程，某规划部门在三市的交界处拟建一个大型环保生态公园，并在公园入口处的东南方位建造一个供市民休闲健身的小型绿化广场，如图是步行小道设计方案示意图，其中，Ox，Oy分别表示自西向东，自南向北的两条主干道，设计方案是自主干道交汇点O处修一条步行小道，小道为抛物线y=x2的一段，在小道上依次以点P1(x1，y1)，P2(x2，y2)，…，P(xn，yn)(n≥10，n∈N*)为圆心，修一系列圆型小道，且这些圆型小道与主干道Ox分别于相切于A1，A2，…，An，…，且任意相邻的两圆彼此外切，若x1=1（单位：百米），且xn+1＜xn．（1）记⊙P1，⊙P2，…，⊙Pn，…的半径rn组成的数列为{rn}，求通项公式rn；
（2）若修建这些圆形小道工程预算总费用为50万元，根据以往施工经验可知，面积为S的圆形小道的实际施工费用为10
| πS |
对于数列{xn}，如果存在一个正整数m，使得对任意的n（n∈N*）都有xn+m=xn成立，那么就把这样一类数列{xn}称作周期为m的周期数列，m的最小值称作数列{xn}的最小正周期，以下简称周期．例如当xn=2时，{xn}是周期为1的周期数列，当yn=sin(
n)时，{yn}的周期为4的周期数列．
（1）设数列{an}满足an+2=λ•an+1-an（n∈N*），a1+a，a2=b（a，b不同时为0），且数列{an}是周期为3的周期数列，求常数λ的值；
（2）设数列{an}的前n项和为Sn，且4Sn=（an+1）2．
①若an＞0，试判断数列{an}是否为周期数列，并说明理由；
②若anan+1＜0，试判断数列{an}是否为周期数列，并说明理由．
（3）设数列{an}满足an+2=-an+1-an（n∈N*），a1=1，a2=2，bn=an+1，数列{bn}的前n项和Sn，试问是否存在p、q，使对任意的n∈N*都有p≤
≤q成立，若存在，求出p、q的取值范围；不存在，说明理由．
查看习题详情和答案>>
| π |
| 2 |
（1）设数列{an}满足an+2=λ•an+1-an（n∈N*），a1+a，a2=b（a，b不同时为0），且数列{an}是周期为3的周期数列，求常数λ的值；
（2）设数列{an}的前n项和为Sn，且4Sn=（an+1）2．
①若an＞0，试判断数列{an}是否为周期数列，并说明理由；
②若anan+1＜0，试判断数列{an}是否为周期数列，并说明理由．
（3）设数列{an}满足an+2=-an+1-an（n∈N*），a1=1，a2=2，bn=an+1，数列{bn}的前n项和Sn，试问是否存在p、q，使对任意的n∈N*都有p≤
| Sn |
| n |
上,且Pn的横坐标构成以
为首项,-1为公差的等差数列{xn}.
+
+…+
＜
;