题目内容
在直角坐标平面上有一点列Pn(xn,yn)(n∈N*),点Pn位于直线y=3x+(1)求点Pn的坐标;
(2)设抛物线列C1,C2,…,Cn,…中的每一条的对称轴都垂直于x轴,第n条抛物线Cn的顶点为Pn,且经过点Dn(0,n2+1)(n∈N*).记与抛物线Cn相切于点Dn的直线的斜率为kn,求证:![]() +
+![]() +…+
+…+![]() <
<![]() ;
;
(3)设S={x|x=2xn,n∈N*},T={y|y=4yn,n∈N*},等差数列{an}的任意一项an∈S∩T,其中a1是S∩T中的最大数,且-256<a10<-125,求数列{an}的通项公式.
解:(1)xn=![]() +(n-1)×(-1)=-n
+(n-1)×(-1)=-n![]() =
=![]() ,
,
∴yn=3·xn+![]() =-3n
=-3n![]() =
=![]() .
.
∴Pn(![]() ,
,![]() ).
).
(2)证明:∵Cn的对称轴垂直于x轴,且顶点为Pn,
设Cn的方程为y=a(x+![]() )2
)2![]() .
.
把Dn(0,n2+1)代入上式,得a=1.
∴Cn的方程为y=x2+(2n+3)x+n2+1.
∴kn=y′|x=0=2n+3.
∴![]() =
=![]() =
=![]() (
(![]() ).
).
∴![]() +
+![]() +…+
+…+![]() =
=![]() [(
[(![]() )+(
)+(![]() )+…+(
)+…+(![]() )]
)]
=![]() (
(![]() )=
)=![]() <
<![]() .
.
(3)S={x|x=-(2n+3),n∈N*},
T={y|y=-(12n+5),n∈N*}={y|y=-2(6n+5)-3,n∈N*},
∴S∩T=T,T中的最大数a1=-17.
设{an}的公差为d,则a10=-17+9d∈(-265,-125),由此得![]() <d<-12.
<d<-12.
又∵an∈T,∴d=-12m(m∈N*).
∴d=-24.∴an=7-24n(n∈N*).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
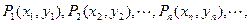 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数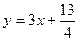 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以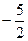 为首项,-1为公差的等
为首项,-1为公差的等 差数列{xn}.
差数列{xn}.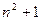 ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求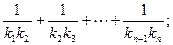
 设
设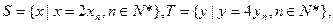 等差数列
等差数列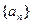 的任一项
的任一项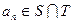 ,其中
,其中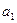 是
是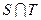 中的最大数,
中的最大数,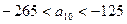 ,求数列
,求数列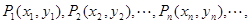 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数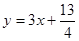 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以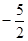 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}. ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求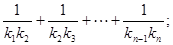
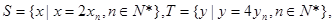 等差数列
等差数列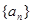 的任一项
的任一项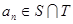 ,其中
,其中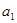 是
是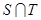 中的最大数,
中的最大数,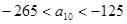 ,求数列
,求数列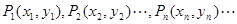 ,对一切正整数
,对一切正整数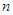 ,点
,点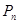 位于函数
位于函数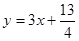 的图象上,且
的图象上,且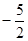 为首项,
为首项,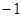 为公差的等差数列
为公差的等差数列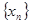 。
。 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于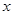 轴,第
轴,第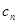 的顶点为
的顶点为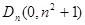 ,记与数列
,记与数列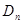 的直线的斜率为
的直线的斜率为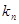 ,求:
,求: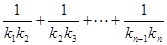 。
。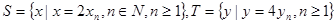 ,等差数列
,等差数列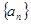 的任一项
的任一项 ,其中
,其中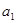 是
是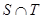 中的最大数,
中的最大数,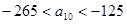 ,求
,求