摘要:[例1]如图,在平行六面体中,是的中点. 求证:(1)∥面. (2)设E.F.G.H.K.L依次是棱AB.BC.CC1.C1D1.D1A1.A1A的中点.则这六点共面. 分析:只需证明与面中的一组基向量共面. 证明(1):设 因为为平行四边形, ,又O是的中点, 若存在实数使成立,则 因为向量不共线, ,. 所以是共面向量, 因为不在所确定的平面内, ∥面,又面, ∥面. (2) 不共线.可作为基底.再依次证明.-能用这组基底表示即可.试试如何? [例2] 在三棱锥S-ABC中.∠SAB=∠SAC=∠ACB=90°.AC=2.BC=.SB=. (1)求证:SC⊥BC, (2)求SC与AB所成角的余弦值. (3)若E.F.G分别是AB.AC.SB的中点. 求证:平面EFG⊥平面ACG.. 思路1:要用向量来研究线面的位置关系.需要有一组基底把有关的向量表示出来.再用向量运算的几何意义来研究. 解法1:(1)设.由已知得: . . (2) 所以SC与AB所成的角为arccos. (3) 思路2:图中垂直关系较为明显.容易建立坐标系的.可以建立空间直角坐标系.利用向量的代数运算来研究. 解法2:如下图.取A为原点.AD.AC.AS分别为x.y.z轴建立空间直角坐标系.则由AC=2.BC=.SB=.得C.B(.2.0).S(0.0.2). =(0.2.-2).=(.0.0). (1)∵=0.∴SC⊥BC. (2)设SC与AB所成的角为θ. ∵=(.2.0).·=4.||| |=4.∴cosθ=.即为所求. (3) , 思悟提练1.利用空间向量可以解决立体几何中的线线垂直.线线平行.四点共面.求长度.求夹角等问题.
网址:http://m.1010jiajiao.com/timu_id_3969706[举报]
 如图在平行六面体ABCD-A1B1C1D1中,E、F、G分别是A1D1、D1D、D1C1的中点.
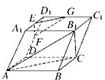
如图在平行六面体ABCD-A1B1C1D1中,E、F、G分别是A1D1、D1D、D1C1的中点.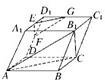 如图在平行六面体ABCD-A1B1C1D1中,E、F、G分别是A1D1、D1D、D1C1的中点.
如图在平行六面体ABCD-A1B1C1D1中,E、F、G分别是A1D1、D1D、D1C1的中点.
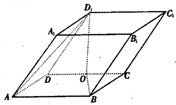 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.