题目内容
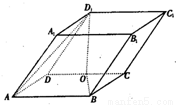
如图在平行六面体ABCD-A1B1C1D1中，E、F、G分别是A1D1、D1D、D1C1的中点．求证：平面EFG∥平面AB1C．
分析：欲证平面EFG∥平面AB1C，根据面面平行的判定定理可知只需在一个平面内找两相交直线与另一平面平行，设
=a，
=b，
=c，然后将
、
、
、
分别利用基底进行表示，然后根据共线定理进行判定，从而得到面面平行的判定定理的条件．
| AB |
| AD |
| AA1 |
| EG |
| AC |
| EF |
| B1C |
解答：
证明：设
=a，
=b，
=c，则
=
+
=
（a+b），
=a+b=2
，
∴
∥
，
=
+
=
b-
c=
（b-c），
=
+
=b-c=2
，
∴
∥
．
又∵EG与EF相交，AC与B1C相交，
∴平面EFG∥平面AB1C．
证明：设| AB |
| AD |
| AA1 |
| EG |
| ED1 |
| D1G |
| 1 |
| 2 |
| AC |
| EG |
∴
| EG |
| AC |
| EF |
| ED1 |
| D1F |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| B1C |
| B1C1 |
| C1C |
| EF |
∴
| EF |
| B1C |
又∵EG与EF相交，AC与B1C相交，
∴平面EFG∥平面AB1C．
点评：本题主要考查了平面与平面平行的判定，以及利用向量的方法证明两直线平行等有关知识，属于基础题．
练习册系列答案
相关题目
对于向量a，b，定义a×b为向量a，b的向量积，其运算结果为一个向量，且规定a×b的模|a×b|=|a||b|sinθ（其中θ为向量a与b的夹角），a×b的方向与向量a，b的方向都垂直，且使得a，b，a×b依次构成右手系．如图，在平行六面体ABCD-EFGH中，∠EAB=∠EAD=∠BAD=60°，AB=AD=AE=2，则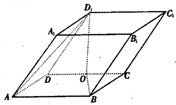
如图，平行六面体ABCD-A1B1C1D1中，AB=2，AD=1，底面ABCD是矩形，顶点D1在底面ABCD上的射影O恰好是CD的中点．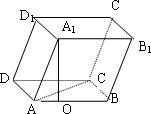
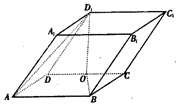如图，平行六面体ABCD-A1B1C1D1中，AB=2，AD=1，底面ABCD是矩形，顶点D1在底面ABCD上的射影O恰好是CD的中点．