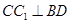题目内容
 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.(I)求证:BO⊥AD1;
(II)若二面角D1-AB-D的大小为60°,求AD1与底面ABCD所成的角.
分析:(I)由顶点D1在底面ABCD上的射影O是CD的中点,我们根据线面垂直的性质,易得OD1⊥OB,又根据等腰三角形三线合一的性质,可得OB⊥OA,进而由线面垂直的性质得到BO⊥平面D1AO,从而BO⊥AD1;
(II)由(I)知D1O⊥底面ABCD,连接AO,则∠D1AO为AD1与底面ABCD所成的角,过O作OH⊥AB,连接D1H,则D1H⊥AB,则∠D1HO=60°,在直角△D1HO中,利用tan∠D1AO=
,可求AD1与底面ABCD所成的角.
(II)由(I)知D1O⊥底面ABCD,连接AO,则∠D1AO为AD1与底面ABCD所成的角,过O作OH⊥AB,连接D1H,则D1H⊥AB,则∠D1HO=60°,在直角△D1HO中,利用tan∠D1AO=
| D1O |
| AO |
解答:证明:(I))∵D1在平面ABCD上的射影为O,
∴OD1⊥平面ABCD,
∴OD1⊥OB
∵点O为DC的中点,DC=2,
∴OC=1,
又∵BC=1,∠DCB=90°,
∴OB⊥OA
∵D1O∩AO=O,
∴OB⊥平面D1AO
∵AD1?平面D1AO
∴BO⊥AD1;
(II)由(I)知D1O⊥底面ABCD,连接AO,则∠D1AO为AD1与底面ABCD所成的角
过O作OH⊥AB,连接D1H,则D1H⊥AB
∴∠D1HO为二面角D1-AB-D的平面角,即∠D1HO=60°
因为底面是矩形,O是CD的中点
所以OH=AD=1
在直角△D1OH中,DO=OH•tan∠D1HO=
在直角△AOH中,AO=
=
故在直角△D1HO中,tan∠D1AO=
=
∴AD1与底面ABCD所成的角为arctan
∴OD1⊥平面ABCD,
∴OD1⊥OB
∵点O为DC的中点,DC=2,
∴OC=1,
又∵BC=1,∠DCB=90°,
∴OB⊥OA
∵D1O∩AO=O,
∴OB⊥平面D1AO
∵AD1?平面D1AO
∴BO⊥AD1;
(II)由(I)知D1O⊥底面ABCD,连接AO,则∠D1AO为AD1与底面ABCD所成的角
过O作OH⊥AB,连接D1H,则D1H⊥AB

∴∠D1HO为二面角D1-AB-D的平面角,即∠D1HO=60°
因为底面是矩形,O是CD的中点
所以OH=AD=1
在直角△D1OH中,DO=OH•tan∠D1HO=
| 3 |
在直角△AOH中,AO=
| OH2+AH2 |
| 2 |
故在直角△D1HO中,tan∠D1AO=
| D1O |
| AO |
| ||
| 2 |
∴AD1与底面ABCD所成的角为arctan
| ||
| 2 |
点评:本题以平行六面体为载体,考查线面垂直,考查线线垂直,同时考查线面角,线线角,解题的关键是正确运用线面垂直的判定与性质,正确作出面面角,线面角.

练习册系列答案
相关题目
 如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为
如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为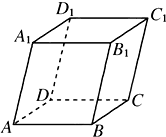 如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,