题目内容

如图,在平行六面体ABCD—A1B1C1D1中,E、F、G分别是A1D1、D1D、D1C1的中点,求证:平面EFG∥平面AB1C.

证明:设

则

而

故∥,即EG∥AC.

又

而

∴∥,即EF∥B1C.

又∵EG∩EF=E,AC∩B1C=C,

∴平面EFG∥平面AB1C.

练习册系列答案
相关题目
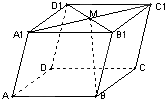精英家教网如图：在平行六面体ABCD-A1B1C1D1中，M为A1C1与B1D1的交点．若
AB
=
a
，
AD
=
b
，
AA1
=
c
，则下列向量中与
BM
相等的向量是（　　）
A、-
1
2
a
+
1
2
b
+
c
B、
1
2
a
+
1
2
b
+
c
C、-
1
2
a
-
1
2
b
+
c
D、
1
2
a-
1
2
b+c
精英家教网如图，在平行六面体ABCD-A1B1C1D1中，已知
AB
=a，
AD
=b，
AA1
=c，则用向量
a
，
b
，
c
可表示向量
BD1
=（　　）
A、
a
+
b
+
c
B、
a
-
b
+
c
C、
a
+
b
-
c
D、-
a
+
b
-
c
精英家教网对于向量a，b，定义a×b为向量a，b的向量积，其运算结果为一个向量，且规定a×b的模|a×b|=|a||b|sinθ（其中θ为向量a与b的夹角），a×b的方向与向量a，b的方向都垂直，且使得a，b，a×b依次构成右手系．如图，在平行六面体ABCD-EFGH中，∠EAB=∠EAD=∠BAD=60°，AB=AD=AE=2，则(
AB
×
AD
)•
AE
=（　　）
A、4
B、8
C、2
2
D、4
2
精英家教网如图，在平行六面体ABCD-A1B1C1D1中，若
AB
=
a
，
AD
=
b
，
AA1
=
c
，则
D1B
=（　　）
A、
a
+
b
-
c
B、
a
+
b
+
c
C、
a
-
b
-
c
D、-
a
+
b
+
c
（2001•上海）如图，在平行六面体ABCD-A1B1C1D1中，M为AC与BD的交点，若
A1B1
=
a
，
A1D1
=
b
，
A1A
=
c
．则下列向量中与
B1M
相等的向量是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网