摘要: 如图3-1.设AB=a,AC=b,AD=c,那么 图3-1 △ABC,△ABD,△ACD面积之和怎样表示? (几乎每个人都能够写出: )
网址:http://m.1010jiajiao.com/timu_id_3951714[举报]
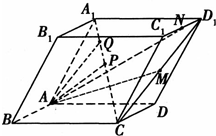 如图所示,在各个面都是平行四边形的四棱柱ABCD-A1B1C1D1中,P是CA1的中点,M是CD1的中点,N是C1D1的中点,点Q在CA1上,且CQ:QA1=4:1,设
如图所示,在各个面都是平行四边形的四棱柱ABCD-A1B1C1D1中,P是CA1的中点,M是CD1的中点,N是C1D1的中点,点Q在CA1上,且CQ:QA1=4:1,设| AB |
| AD |
| AA1 |
(1)
| AP |
(2)
| AM |
(3)
| AN |
(4)
| AQ |
 (2012•安徽模拟)已知矩形ABCD中,AB=3,AD=2,点E在CD上且CE=1(如图(1)).把△DAE沿AE向上折起到D'AE的位置,使二面角D'-AE-B的大小为120°(如图(2)).
(2012•安徽模拟)已知矩形ABCD中,AB=3,AD=2,点E在CD上且CE=1(如图(1)).把△DAE沿AE向上折起到D'AE的位置,使二面角D'-AE-B的大小为120°(如图(2)).(Ⅰ)求四棱锥D'-ABCE的体积;
(Ⅱ)求CD'与平面ABCE所成角的正切值;
(Ⅲ)设M为CD'的中点,是否存在棱AB上的点N,使MN∥平面D'AE?若存在,试求出N点位置;若不存在,请说明理由.
(2011•莆田模拟)如图(1),在直角梯形ACC1A1中,∠CAA1=90°,AA1∥CC1,AA1=4,AC=3,CC1=1,点B在线段AC上,AB=2BC,BB1∥AA1,且BB1交A1C1于点B1.现将梯形ACC1A1沿直线BB1折成二面角A-BB1-C,设其大小为θ.
(1)在上述折叠过程中,若90°≤θ≤180°,请你动手实验并直接写出直线A1B1与平面BCC1B1所成角的取值范围.(不必证明);
(2)当θ=90°时,连接AC、A1C1、AC1,得到如图(2)所示的几何体ABC-A1B1C1,
(i)若M为线段AC1的中点,求证:BM∥平面A1B1C1;
(ii)记平面A1B1C1与平面BCC1B1所成的二面角为α(0<α≤90°),求cosa的值.


查看习题详情和答案>>
(1)在上述折叠过程中,若90°≤θ≤180°,请你动手实验并直接写出直线A1B1与平面BCC1B1所成角的取值范围.(不必证明);
(2)当θ=90°时,连接AC、A1C1、AC1,得到如图(2)所示的几何体ABC-A1B1C1,
(i)若M为线段AC1的中点,求证:BM∥平面A1B1C1;
(ii)记平面A1B1C1与平面BCC1B1所成的二面角为α(0<α≤90°),求cosa的值.


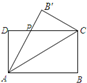 (2013•南通一模)某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB'交DC于点P.当△ADP的面积最大时最节能,凹多边形ACB'PD的面积最大时制冷效果最好.
(2013•南通一模)某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB'交DC于点P.当△ADP的面积最大时最节能,凹多边形ACB'PD的面积最大时制冷效果最好.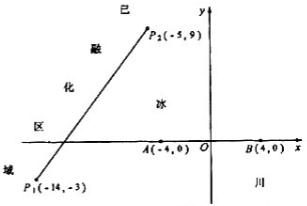 为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(如图).考察范围到A、B两点的距离之和不超过10Km的区域.
为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(如图).考察范围到A、B两点的距离之和不超过10Km的区域.