摘要:22.已知:均是正数.且.求证:, (2)当均是正数.且.对真分数.给出类似上小题的结论.并予以证明, (3)证明:△中.小题结论) (4)自己设计一道可直接应用第小题结论的不等式证明题.并写出证明过程.
网址:http://m.1010jiajiao.com/timu_id_3937073[举报]
(1)已知: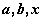 均是正数,且
均是正数,且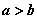 ,求证:
,求证: ;
;
(2)当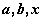 均是正数,且
均是正数,且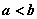 ,对真分数
,对真分数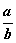 ,给出类似上小题的结论,并予以证明;
,给出类似上小题的结论,并予以证明;
(3)证明:△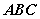 中,
中,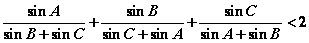 (可直接应用第(1)、(2)小题结论)
(可直接应用第(1)、(2)小题结论)
(4)自己设计一道可直接应用第(1)、(2)小题结论的不等式证明题,并写出证明过程.
查看习题详情和答案>>
已知各项均为正数的两个无穷数列{an}、{bn}满足anbn+1+an+1bn=2nan+1(n∈N*).
(Ⅰ)当数列{an}是常数列(各项都相等的数列),且b1=
时,求数列{bn}的通项公式;
(Ⅱ)设{an}、{bn}都是公差不为0的等差数列,求证:数列{an}有无穷多个,而数列{bn}惟一确定;
(Ⅲ)设an+1=
(n∈N*),Sn=
bi,求证:2<
<6.
查看习题详情和答案>>
(Ⅰ)当数列{an}是常数列(各项都相等的数列),且b1=
| 1 |
| 2 |
(Ⅱ)设{an}、{bn}都是公差不为0的等差数列,求证:数列{an}有无穷多个,而数列{bn}惟一确定;
(Ⅲ)设an+1=
| 2an2+an |
| an+1 |
| 2n |
 |
| i=1 |
| Sn |
| n2 |
已知函数f(x)的定义域为R,对任意实数m、n,均有f(m+n)=f(m)+f(n)-1,且f(-![]() )=0,当x>-
)=0,当x>-![]() 时,有
时,有
f(x)>0.
(1)求证:f(x)是单调递增函数;
(2)解不等式1+f(![]() )≤f(1)+f(ax),其中a为正常数.
)≤f(1)+f(ax),其中a为正常数.
 时,求数列{bn}的通项公式;
时,求数列{bn}的通项公式; ,Sn=
,Sn=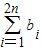 ,求证:2<
,求证:2<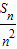 <6.
<6.