摘要:18. 如图.直线l1:与直线l2:之间的阴影区域记为W.其左半部分记为W1.右半部分记为W2. (Ⅰ)分别用不等式组表示W1和W2, (Ⅱ)若区域W中的动点P(x.y)到l1.l2的距离之积等于d2.求点P的轨迹C的方程, (Ⅲ)设不过原点O的直线l与(Ⅱ)中的曲线C相交于M1.M2两点.且与l1.l2分别 交于M3.M4两点. 求证△OM1M2的重心与△OM3M4的重心重合. [答案] [详解] 解:(I) (II)直线直线,由题意得 即 由知 所以即 所以动点P的轨迹方程为 (III)当直线与轴垂直时,可设直线的方程为由于直线.曲线C关于轴对称, 且与关于轴对称,于是的中点坐标都为,所以 的重心坐标都为,即它们的重心重合. 当直线与轴不垂直时,设直线的方程为 由,得 由直线 与曲线C有两个不同交点,可知,且 设的坐标分别为 则 设的坐标分别为 由 从而 所以 所以 于是的重心与的重心也重合. [名师指津] 本题为解析几何的综合题型,在高考试题中解析经常会与函数.数列.不等式.向量等综合考 查各种数学思想及方法.
网址:http://m.1010jiajiao.com/timu3_id_4469045[举报]
 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是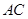 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.
