在探究向心力与质量、转速和半径的关系的实验中,得到如下数据.试根据表中数据分析说明向心力的大小与哪些因素有关.
| m/kg | r/m F n/(r/s) |
0.2 | 0.4 |
| 1 | 1 | F | 2F |
| 1 | 2 | 4F | 8F |
| 2 | 2 | 8F | 16F |
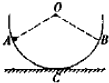 如图所示,质量为M的半圆弧槽放置于粗糙水平地面上,半圆弧面光滑,O为圆弧槽圆心.质量为m的小球从圆弧槽上的A点静止释放,OA连线与竖直方向成60°角,小球在圆弧槽上的A、B之间来回运动,半圆槽始终静止,则下列说法正确的是( )
如图所示,质量为M的半圆弧槽放置于粗糙水平地面上,半圆弧面光滑,O为圆弧槽圆心.质量为m的小球从圆弧槽上的A点静止释放,OA连线与竖直方向成60°角,小球在圆弧槽上的A、B之间来回运动,半圆槽始终静止,则下列说法正确的是( )| A、小球运动到B点时,地面对圆弧槽有向左的摩擦力 | B、小球运动到B点时,圆弧槽对地面的压力大小为FN=(M+m)g | C、小球运动到C点时,圆弧槽对地面的压力大小为FN=(M+m)g | D、小球运动到C点时,圆弧槽对地面的压力大小为FN=(M+2m)g |
 如图所示,长度不同的两根轻绳L1与L2,一端分别连接质量为m1和m2的两个小球,另一端悬于天花板上的同一点O,两小球质量之比m1:m2=1:2,两小球在同一水平面内做匀速圆周运动,绳L1,L2与竖直方向的夹角分别为30°与60°,下列说法中正确的是( )
如图所示,长度不同的两根轻绳L1与L2,一端分别连接质量为m1和m2的两个小球,另一端悬于天花板上的同一点O,两小球质量之比m1:m2=1:2,两小球在同一水平面内做匀速圆周运动,绳L1,L2与竖直方向的夹角分别为30°与60°,下列说法中正确的是( )| A、绳L1,L2的拉力大小之比为1:3 | B、小球m1,m2运动的向心力大小之比为1:6 | C、小球m1,m2运动的周期之比为2:1 | D、小球m1,m2运动的线速度大小之比为1:2 |
 做圆周运动的两个物体M和N,它们所受的向心力F与轨道半径R之间的关系如图所示,其中与N对应的图线是过坐标原点的直线,与M对应的图线为双曲线的一个分支,则以下推断正确的是( )
做圆周运动的两个物体M和N,它们所受的向心力F与轨道半径R之间的关系如图所示,其中与N对应的图线是过坐标原点的直线,与M对应的图线为双曲线的一个分支,则以下推断正确的是( )| A、若两者R相同,则角速度ωM一定等于ωN | B、若两者F大小相等,动能EkM一定等于EKN | C、若质量mM大于mN,且向心力均等于F′,则线速度vM一定小于vN | D、在两图线的交点,动能EkM一定等于EkN |
“旋转秋千”是游乐园里常见的游乐项目,其基本装置是将绳子上端固定在转盘的边上,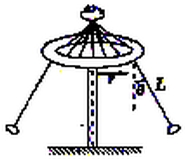 绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看质点,“旋转秋千”可简化为如图所示的模型.其中,处于水平面内的圆形转盘,半径为r,可绕穿过其中心的竖直轴转动.让转盘由静止开始逐渐加速转动,经过一段时间后质点与转盘一起以角速度ω做匀速圆周运动,此时绳子与竖直方向的夹角为θ.已知绳长为L且不可伸长,质点的质量为m,不计空气阻力及绳重.则下列说法中正确的是( )
绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看质点,“旋转秋千”可简化为如图所示的模型.其中,处于水平面内的圆形转盘,半径为r,可绕穿过其中心的竖直轴转动.让转盘由静止开始逐渐加速转动,经过一段时间后质点与转盘一起以角速度ω做匀速圆周运动,此时绳子与竖直方向的夹角为θ.已知绳长为L且不可伸长,质点的质量为m,不计空气阻力及绳重.则下列说法中正确的是( )
 绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看质点,“旋转秋千”可简化为如图所示的模型.其中,处于水平面内的圆形转盘,半径为r,可绕穿过其中心的竖直轴转动.让转盘由静止开始逐渐加速转动,经过一段时间后质点与转盘一起以角速度ω做匀速圆周运动,此时绳子与竖直方向的夹角为θ.已知绳长为L且不可伸长,质点的质量为m,不计空气阻力及绳重.则下列说法中正确的是( )
绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看质点,“旋转秋千”可简化为如图所示的模型.其中,处于水平面内的圆形转盘,半径为r,可绕穿过其中心的竖直轴转动.让转盘由静止开始逐渐加速转动,经过一段时间后质点与转盘一起以角速度ω做匀速圆周运动,此时绳子与竖直方向的夹角为θ.已知绳长为L且不可伸长,质点的质量为m,不计空气阻力及绳重.则下列说法中正确的是( )| A、质点的重力越大,绳子与竖直方向的夹角θ越小 | ||||
| B、质点做匀速圆周运动的向心力是其所受悬线的拉力 | ||||
C、转盘转动的角速度ω与夹角θ的关系为ω=
| ||||
D、质点从静止到做匀速圆周运动的过程中,绳子对质点做的功为
|
 在匀速转动的水平圆盘上有一个相对转盘静止的物体,则物体相对于转盘的运动趋势是( )
在匀速转动的水平圆盘上有一个相对转盘静止的物体,则物体相对于转盘的运动趋势是( )| A、没有相对运动趋势 | B、沿切线方向 | C、沿半径指向圆心 | D、沿半径背离圆心 |
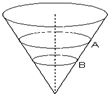 一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定,有质量不相等的小球A和B沿着筒的内壁在水平面内作匀速圆周运动,如图所示,A的运动半径较大,则( )
一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定,有质量不相等的小球A和B沿着筒的内壁在水平面内作匀速圆周运动,如图所示,A的运动半径较大,则( )| A、A球的线速度必小于B球的线速度 | B、A球的角速度必小于B球的角速度 | C、A球需要的向心力等于B球需要的向心力 | D、A球对筒壁的压力可能等于B球对筒壁的压力 |
 如图所示,A是半径为r的圆形光滑轨道,固定在木板B上,竖直放置;B的左右两侧各有一光滑挡板固定在地面上,使其不能左右运动,小球C静止放在轨道最低点,A,B,C质量相等.现给小球一水平向右的初速度v0,使小球在圆型轨道的内侧做圆周运动,为保证小球能通过轨道的最高点,且不会使B离开地面,初速度v0必须满足( )(重力加速度为g)
如图所示,A是半径为r的圆形光滑轨道,固定在木板B上,竖直放置;B的左右两侧各有一光滑挡板固定在地面上,使其不能左右运动,小球C静止放在轨道最低点,A,B,C质量相等.现给小球一水平向右的初速度v0,使小球在圆型轨道的内侧做圆周运动,为保证小球能通过轨道的最高点,且不会使B离开地面,初速度v0必须满足( )(重力加速度为g)A、最小值为
| ||
B、最大值为
| ||
C、最小值为
| ||
D、最大值为
|
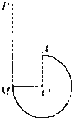 如图所示,四分之三的半径为R圆弧轨道固定在地面上,半径AO竖直,有一质量为m的小球(可视为质点)从离M点3R的P点处做自由下落,从圆弧轨道的M点无能量损失的进入轨道,运动到A点时恰好对轨道无压力(重力加速度为g,不计空气阻力),则( )
如图所示,四分之三的半径为R圆弧轨道固定在地面上,半径AO竖直,有一质量为m的小球(可视为质点)从离M点3R的P点处做自由下落,从圆弧轨道的M点无能量损失的进入轨道,运动到A点时恰好对轨道无压力(重力加速度为g,不计空气阻力),则( )A、P→A过程,合力做功为
| ||
B、P→A过程,机械能减小
| ||
C、P→A过程,摩擦力做功
| ||
| D、小球从A点飞出后,还能进入圆轨道 |
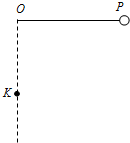 如图所示,长度为l的细线,一端固定于O点,另一端拴一小球,先将线拉直呈水平,使小球位于P点,然后无初速释放小球,当小球运动到最低点时,悬线遇到在O点正下方水平固定着的钉子K,不计任何阻力,若要求小球能绕钉子在竖直面内做完整圆周运动,则K与O点的距离可以是( )
如图所示,长度为l的细线,一端固定于O点,另一端拴一小球,先将线拉直呈水平,使小球位于P点,然后无初速释放小球,当小球运动到最低点时,悬线遇到在O点正下方水平固定着的钉子K,不计任何阻力,若要求小球能绕钉子在竖直面内做完整圆周运动,则K与O点的距离可以是( )A、
| ||
B、
| ||
C、
| ||
D、
|