题目内容
5.某星球的半径是地球半径的p倍,质量是地球质量的q倍,已知地球表面的重力加速度为g,地球上的第一宇宙速度为v,求:(1)该星球表面的重力加速度;
(2)该星球的“第一宇宙速度”.
分析 (1)根据万有引力等于重力,结合星球和地球的质量之比、半径之比求出星球表面的重力加速度,从而得出星球表面的重力加速度.
(2)根据万有引力提供向心力得出第一宇宙速度的表达式,从而结合星球和地球的质量之比和半径之比求出第一宇宙速度之比,求出星球的第一宇宙速度.
解答 解:(1)在地球表面,物体所受的重力近似等于物体所受的万有引力,
有:$G\frac{M{m}_{1}}{{R}^{2}}={m}_{1}g$,
同样在星球表面:$G\frac{{M}_{星}{m}_{2}}{{{R}_{星}}^{2}}={m}_{2}{g}_{星}$,
解得$\frac{g}{{g}_{星}}=\frac{M}{{M}_{星}}•\frac{{{R}_{星}}^{2}}{{R}^{2}}=\frac{{p}^{2}}{q}$.
则星球表面的重力加速度g星=$\frac{qg}{{p}^{2}}$.
(2)地球上的第一宇宙速度 $\frac{GM{m}_{1}}{{R}^{2}}={m}_{1}\frac{{v}^{2}}{R}$,
解得v=$\sqrt{\frac{GM}{R}}$,
同样,在星球上第一宇宙速度 ${v}_{星}=\sqrt{\frac{G{M}_{星}}{{R}_{星}}}$,
解得$\frac{{v}_{星}}{v}=\sqrt{\frac{{M}_{星}R}{M{R}_{星}}}=\sqrt{\frac{q}{p}}$,
则${v}_{星}=v\sqrt{\frac{q}{p}}$.
答:(1)该星球表面的重力加速度为$\frac{qg}{{p}^{2}}$.;
(2)该星球的“第一宇宙速度”为$v\sqrt{\frac{q}{p}}$.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

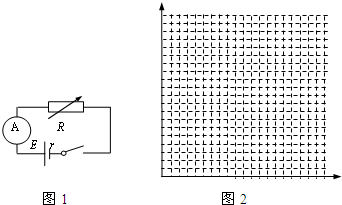
| 次数 | 1 | 2 | 3 | 4 | 5 |
| R(Ω) | 4.0 | 10.0 | 16.0 | 22.0 | 28.0 |
| I(A) | 1.00 | 0.50 | 0.34 | 0.25 | 0.20 |
| $\frac{1}{I}$(A-1) | 1.0 | 2.0 | 2.9 | 4.0 | 5.0 |
(2)利用测得的数据在图2中的坐标纸上画出适当的图象;
(3)由图象可知,该电池的电动势E=6V,内阻r=2.0Ω.
| A. | 加速运动时人对沼泽地的压力大于沼泽地对他的支持力 | |
| B. | 加速运动时人对沼泽地的压力小于沼泽地对他的支持力 | |
| C. | 人对沼泽地的压力先大于后等于沼泽地对他的支持力 | |
| D. | 人对沼泽地的压力大小总等于沼泽地对他的支持力 |
| A. | 地球的质量 | B. | 月球的质量 | ||
| C. | 月球运动的向心加速度 | D. | 月球表面的重力加速度 |
| A. | F | B. | 2F | C. | $\frac{F}{2}$ | D. | $\frac{F}{4}$ |
| A. | 在平衡力作用下,物体可以做曲线运动 | |
| B. | 曲线运动的加速度可以一直为零 | |
| C. | 曲线运动一定是变速运动 | |
| D. | 在恒力作用下,物体不可以做曲线运动 |