题目内容
16. 有一条沿逆时针方向匀速传送的浅色传送带,其恒定速度v=2m/s,传送带与水平面的夹角θ=37°,传送带上下两端AB间距离l=6m,如图所示,现有一可视为质点的煤块以v=2m/s的初速度从AB的中点向上运动,煤块与传送带之间的动摩擦因数μ=0.5,滑轮大小可忽略不计,求煤块最终在传送带上留下的黑色痕迹的长度.已知g取10m/s2,sin37°=0.6,cos37°=0.8.
有一条沿逆时针方向匀速传送的浅色传送带,其恒定速度v=2m/s,传送带与水平面的夹角θ=37°,传送带上下两端AB间距离l=6m,如图所示,现有一可视为质点的煤块以v=2m/s的初速度从AB的中点向上运动,煤块与传送带之间的动摩擦因数μ=0.5,滑轮大小可忽略不计,求煤块最终在传送带上留下的黑色痕迹的长度.已知g取10m/s2,sin37°=0.6,cos37°=0.8.
分析 根据牛顿第二定律分别求出煤块上升和下滑过程中的加速度大小,根据运动学公式分段求出煤块相对于皮带的位移大小,最后分析留下的轨迹长度.
解答 解:滑块沿斜面向上运动的加速度为:${a}_{1}=\frac{mgsinθ+μmgcosθ}{m}=10m/{s}^{2}$,
上升的时间为:${t}_{1}=\frac{v}{a}=0.2s$,
上升过程中的位移为:${x}_{1}=v{t}_{1}-\frac{1}{2}{a}_{1}{t}_{1}^{2}$=0.2m,
此过程中皮带向下的位移为:x′1=vt1=0.4m,
所以相对位移为:△x1=0.2+0.4=0.6m;
物块下降过程中达到与皮带速度相等的时间为:${t}_{2}=\frac{v}{{a}_{1}}=0.2s$,
下降过程中的相对位移为:$△{x}_{2}=v{t}_{2}-(v{t}_{2}+\frac{1}{2}{a}_{1}{t}_{2}^{2})=0.2m$;
回到中点以后煤块继续做加速运动的加速度为:${a}_{2}=\frac{mgsinθ-μmgcosθ}{m}=2m/{s}^{2}$,
煤块最后滑离皮带有:$\frac{l}{2}=v{t}_{3}+\frac{1}{2}{a}_{2}{t}_{3}^{2}$,
解得:t3=1s,
该过程中相对位移为:$△{x}_{3}=v{t}_{3}+\frac{1}{2}a{t}_{3}^{2}-vt=1m$,
故留下的痕迹长度为:△x=△x3=1m.
答:煤块最终在传送带上留下的黑色痕迹的长度为1m.
点评 本题主要是考查传送带问题,解答本题要能够分析煤块的受力情况和运动情况;注意:要求煤块在传送带上留下的痕迹,不能够将各段相对位移相加,由于各段之间的痕迹可能有重合.

 如图,一质量为m,电荷量为q的带负电粒子在匀强电场中运动,A、B为其运动轨迹上的两点.已知该粒子在A点的速度大小为v0,方向与电场方向间的夹角为45°,它运动到B点时速度方向与电场方向间的夹角为30°.下列说法中正确的是(不计重力)( )
如图,一质量为m,电荷量为q的带负电粒子在匀强电场中运动,A、B为其运动轨迹上的两点.已知该粒子在A点的速度大小为v0,方向与电场方向间的夹角为45°,它运动到B点时速度方向与电场方向间的夹角为30°.下列说法中正确的是(不计重力)( )| A. | 电场的方向向右 | B. | A点的电势比B点的电势低 | ||
| C. | 粒子在B点的速度为$\sqrt{3}$v0 | D. | A、B两点间的电势差U=$\frac{m{{v}_{0}}^{2}}{2q}$ |
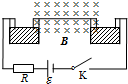 如图所示,一段质量为m的铜导线弯成Π形,它的水平部分长为l处于磁感应强度为B、方向垂直于纸面向里的匀强磁场中.导线的两端竖直部分的下端插入两汞槽内液面下h,两汞槽通过导线分别与内阻可忽略,电动势为ε的电源正负极连接,电路中的电阻为R.合上开关K,当电动势ε足够大时,在磁场的作用下导线便从汞槽内跳离,切断电路.导线上升到一定高度后又开始下落,当导线的下端接触到汞液体后,电路重新接通,在磁场的作用下,导线下落速度逐渐降至零.此后,该段导线又重复上述运动过程,形成周期运动.忽略导线和汞液体的电阻,并设h较小,导线在磁场中运动时的电磁感应亦可忽略,则在一个周期内电源做功为( )
如图所示,一段质量为m的铜导线弯成Π形,它的水平部分长为l处于磁感应强度为B、方向垂直于纸面向里的匀强磁场中.导线的两端竖直部分的下端插入两汞槽内液面下h,两汞槽通过导线分别与内阻可忽略,电动势为ε的电源正负极连接,电路中的电阻为R.合上开关K,当电动势ε足够大时,在磁场的作用下导线便从汞槽内跳离,切断电路.导线上升到一定高度后又开始下落,当导线的下端接触到汞液体后,电路重新接通,在磁场的作用下,导线下落速度逐渐降至零.此后,该段导线又重复上述运动过程,形成周期运动.忽略导线和汞液体的电阻,并设h较小,导线在磁场中运动时的电磁感应亦可忽略,则在一个周期内电源做功为( )| A. | ε2$\sqrt{\frac{2hm}{BεlR-mg{R}^{2}}}$ | B. | ε2$\sqrt{\frac{hm}{BεlR-mg{R}^{2}}}$ | C. | 2ε2$\sqrt{\frac{2hm}{BεlR-mg{R}^{2}}}$ | D. | 2ε2$\sqrt{\frac{hm}{BεlR-mg{R}^{2}}}$ |

| A. | 质点在第1s内做匀速直线运动 | |
| B. | 质点始终向同一方向运动 | |
| C. | 质点在第1s内和第4s内位移之比为1:2 | |
| D. | 质点在第1s内和第4s内平均速度比为1:3 |
 某物体运动的速度-时间图象如图所示,求:
某物体运动的速度-时间图象如图所示,求: