��Ŀ����
8��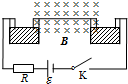 ��ͼ��ʾ��һ������Ϊm��ͭ������ɦ��Σ�����ˮƽ���ֳ�Ϊl���ڴŸ�Ӧǿ��ΪB������ֱ��ֽ���������ǿ�ų��У����ߵ�������ֱ���ֵ��¶˲�����������Һ����h��������ͨ�����߷ֱ�������ɺ��ԣ��綯��Ϊ�ŵĵ�Դ���������ӣ���·�еĵ���ΪR�����Ͽ���K�����綯�Ʀ��㹻��ʱ���ڴų��������µ��߱�ӹ��������룬�жϵ�·������������һ���߶Ⱥ��ֿ�ʼ���䣬�����ߵ��¶˽Ӵ�����Һ���·���½�ͨ���ڴų��������£����������ٶ������㣮�˺öε������ظ������˶����̣��γ������˶������Ե��ߺ�Һ��ĵ��裬����h��С�������ڴų����˶�ʱ�ĵ�Ÿ�Ӧ��ɺ��ԣ�����һ�������ڵ�Դ����Ϊ��������
��ͼ��ʾ��һ������Ϊm��ͭ������ɦ��Σ�����ˮƽ���ֳ�Ϊl���ڴŸ�Ӧǿ��ΪB������ֱ��ֽ���������ǿ�ų��У����ߵ�������ֱ���ֵ��¶˲�����������Һ����h��������ͨ�����߷ֱ�������ɺ��ԣ��綯��Ϊ�ŵĵ�Դ���������ӣ���·�еĵ���ΪR�����Ͽ���K�����綯�Ʀ��㹻��ʱ���ڴų��������µ��߱�ӹ��������룬�жϵ�·������������һ���߶Ⱥ��ֿ�ʼ���䣬�����ߵ��¶˽Ӵ�����Һ���·���½�ͨ���ڴų��������£����������ٶ������㣮�˺öε������ظ������˶����̣��γ������˶������Ե��ߺ�Һ��ĵ��裬����h��С�������ڴų����˶�ʱ�ĵ�Ÿ�Ӧ��ɺ��ԣ�����һ�������ڵ�Դ����Ϊ��������| A�� | ��2$\sqrt{\frac{2hm}{B��lR-mg{R}^{2}}}$ | B�� | ��2$\sqrt{\frac{hm}{B��lR-mg{R}^{2}}}$ | C�� | 2��2$\sqrt{\frac{2hm}{B��lR-mg{R}^{2}}}$ | D�� | 2��2$\sqrt{\frac{hm}{B��lR-mg{R}^{2}}}$ |
���� ���ݱպϵ�·��ŷķ���������·�������������ܵİ��������Ե�����ţ�ٵڶ��������ʱ�䣬���ͨ�����ߵĵ�����һ�����ڼ��������½����̣���Դ���Ĺ�W=2q?
��� �⣺ͨ��������ĵ���$I=\frac{?}{R}$
�������ܰ�����${F}_{��}^{\;}=BIL=B\frac{?}{R}l$
����ţ�ٵڶ����ɣ��У�${F}_{��}^{\;}-mg=ma$
��ã�$a=\frac{B\frac{?}{R}l-mg}{m}=\frac{B?l-mgR}{mR}$
����λ�ƹ�ʽ$h=\frac{1}{2}a{t}_{\;}^{2}$����$t=\sqrt{\frac{2h}{a}}=\sqrt{\frac{2mhR}{B?l-mgR}}$
ͨ���ĵ���$q=It=\frac{?}{R}\sqrt{\frac{2mhR}{B?l-mgR}}$
��һ�����ڵ�Դ����$W=2q?=2?\sqrt{\frac{2mhR}{B?l-mgR}•\frac{1}{{R}_{\;}^{2}}}$•?=$2{?}_{\;}^{2}\sqrt{\frac{2mh}{B?lR-mg{R}_{\;}^{2}}}$
��ѡ��C
���� �������Ĺؼ���Ҫ֪����·�����㶨��֪����Դ��һ���������Ĺ������������½�������ͨ�����ߵĵ����͵�Դ�綯�Ƶij˻���ע����Ե�Ÿ�Ӧ��Ӱ�죬�����Ҫ���Ƿ��綯�ƣ������Ͳ��Ǻ㶨�ģ�

��ϰ��ϵ�д�
 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
�����Ŀ
4��������ͬһ������ֱ���˶�����tʱ����ͨ����λ��Ϊx�����м�λ��$\frac{1}{2}$x�����ٶ�Ϊv1�����м�ʱ��$\frac{1}{2}$t���ٶ�Ϊv2��������
| A�� | �������ȼ���ֱ���˶�ʱ��v1��v2 | B�� | �������ȼ���ֱ���˶�ʱ��v1��v2 | ||
| C�� | �������ȼ���ֱ���˶�ʱ��v1��v2 | D�� | �������ȼ���ֱ���˶�ʱ��v1��v2 |
5��һ�������ֵһ�����������˵ĵ�ѹ��U��ʾ������ĵ�����R��ʾ����������ĵ�����I��ʾ���������ĸ�ͼ������ӳ�Ĺ�ϵ��ȷ���ǣ�������
| A�� |  | B�� |  | C�� |  | D�� |  |
20��һ����Ϊ1kg������ͬʱ�ܵ������������ã����������Ĵ�С�ֱ�Ϊ3N��7N����ô������ļ��ٶȴ�С�������ǣ�������
| A�� | 4m/s2 | B�� | 2m/s2 | C�� | 10m/s2 | D�� | 6m/s2 |
18����ͼ�У����UAB=5V��UBC=5V����VC=-5V�����жϴ˵�·�IJο����ǣ�������


| A�� | A�� | B�� | B�� | C�� | C�� | D�� | ���ж� |
 ��һ������ʱ�뷽�����ٴ��͵�dzɫ���ʹ�����㶨�ٶ�v=2m/s�����ʹ���ˮƽ��ļнǦ�=37�㣬���ʹ���������AB�����l=6m����ͼ��ʾ������һ����Ϊ�ʵ��ú����v=2m/s�ij��ٶȴ�AB���е������˶���ú���봫�ʹ�֮��Ķ�Ħ��������=0.5�����ִ�С�ɺ��Բ��ƣ���ú�������ڴ��ʹ������µĺ�ɫ�ۼ��ij��ȣ���֪gȡ10m/s2��sin37��=0.6��cos37��=0.8��
��һ������ʱ�뷽�����ٴ��͵�dzɫ���ʹ�����㶨�ٶ�v=2m/s�����ʹ���ˮƽ��ļнǦ�=37�㣬���ʹ���������AB�����l=6m����ͼ��ʾ������һ����Ϊ�ʵ��ú����v=2m/s�ij��ٶȴ�AB���е������˶���ú���봫�ʹ�֮��Ķ�Ħ��������=0.5�����ִ�С�ɺ��Բ��ƣ���ú�������ڴ��ʹ������µĺ�ɫ�ۼ��ij��ȣ���֪gȡ10m/s2��sin37��=0.6��cos37��=0.8�� ��ͼ��ʾ��һ����m=2kg��С��������ң�����˻��ӵ����ɾ�ֹ��ʼ��ֱ�����ȼ�����ɣ���ʱ��t1=6sʱ���ٶȴ�Сv1=6m/s��֮����ң����ʹ���˻�����ʧȥ�����������˻����䵽�����ijһ�߶�ʱ����ң����ʹ���˻��������������ʱ��С��ȵ�������������˻���ص���ʱ���ٶ�ǡ��Ϊ�㣬��֪���˻���������������о��ܵ���С��Ϊf=4N�Ŀ���������ȡg=10m/s2����
��ͼ��ʾ��һ����m=2kg��С��������ң�����˻��ӵ����ɾ�ֹ��ʼ��ֱ�����ȼ�����ɣ���ʱ��t1=6sʱ���ٶȴ�Сv1=6m/s��֮����ң����ʹ���˻�����ʧȥ�����������˻����䵽�����ijһ�߶�ʱ����ң����ʹ���˻��������������ʱ��С��ȵ�������������˻���ص���ʱ���ٶ�ǡ��Ϊ�㣬��֪���˻���������������о��ܵ���С��Ϊf=4N�Ŀ���������ȡg=10m/s2����

 ������Ϊ100mA������r1ԼΪ4����
������Ϊ100mA������r1ԼΪ4���� ������Ϊ500 ��A������r2=750����
������Ϊ500 ��A������r2=750����