��Ŀ����
2��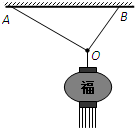 �ҹ����ٵط��ڽ����ڼ��йҺ������ϰ�ף���ͼ������Ϊm�ĵ������������ȳ�������OA��OB������ˮƽ�컨���ϣ�OA��OB����OΪ��㣮�������ٶȴ�СΪg����OA��OB��O��������ֱ�ΪFA��FB�������ܹ������㹻���������������
�ҹ����ٵط��ڽ����ڼ��йҺ������ϰ�ף���ͼ������Ϊm�ĵ������������ȳ�������OA��OB������ˮƽ�컨���ϣ�OA��OB����OΪ��㣮�������ٶȴ�СΪg����OA��OB��O��������ֱ�ΪFA��FB�������ܹ������㹻���������������| A�� | FA����FB | |
| B�� | FA��FB�������mg | |
| C�� | ����������ĵ�����FB����������FA���������� | |
| D�� | ������ε�������A��λ�ã�FA��FB�������ܴ���mg |
���� ��O����������������������������������ƽ����������Ϻϳɷ���������
���  �⣺��O��������������ͼ��ʾ��
�⣺��O��������������ͼ��ʾ��
����ƽ����������������Ҷ������У�
$\frac{{F}_{A}}{sin��}=\frac{{F}_{B}}{sin��}=\frac{G}{sin��180��-��-�£�}$
A�����ڦ����£���$\frac{{F}_{A}}{{F}_{B}}=\frac{sin��}{sin��}��1$����A����
B������ƽ��������FA��FB�ĺ�������mg����B����
C��$\frac{{F}_{A}}{{F}_{B}}=\frac{sin��}{sin��}��1$���ʻ���������ĵ����������¾����䣬����$\frac{{F}_{A}}{{F}_{B}}=\frac{sin��}{sin��}=C=\frac{��{F}_{A}}{��{F}_{B}}$��FB����������FA����������C��ȷ��
D����������A��λ�ã�ʹA�������ƶ�������+������180��ʱ����ʹFA��FB������mg����D����
��ѡ��C
���� ����ؼ�����ȷO�㴦������ƽ��״̬�����ƽ���������ϳɷ������Ҷ�����ʽ�������Ѷ����У�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
12������������������������������˵����ȷ���ǣ�������
| A�� | ��װ������ʱ��Ӧ���õ����������� | |
| B�� | �ɵ�ص����Խ��صĵ綯��ҲԽ�� | |
| C�� | �������洢�ĵ����Խ�������ĵ���ҲԽ�� | |
| D�� | ʹ�ö��õ��������ͬ��ֵ�ĵ���ʱ��һ��Ҫ�ٴ�ŷķ���� |
13�� ��ͼ��ʾ����������Ϊm��A��BС��С����Ϊ�ʵ㣩��ͨ����Ϊl�IJ����쳤����ˮƽ�����������е�����·�H���̶�һ�⻬����O����ͬʱ�����ͷ���С�����������ƣ��������ٶ�Ϊg����С������Ĺ����У�����˵����ȷ���ǣ�������
��ͼ��ʾ����������Ϊm��A��BС��С����Ϊ�ʵ㣩��ͨ����Ϊl�IJ����쳤����ˮƽ�����������е�����·�H���̶�һ�⻬����O����ͬʱ�����ͷ���С�����������ƣ��������ٶ�Ϊg����С������Ĺ����У�����˵����ȷ���ǣ�������
 ��ͼ��ʾ����������Ϊm��A��BС��С����Ϊ�ʵ㣩��ͨ����Ϊl�IJ����쳤����ˮƽ�����������е�����·�H���̶�һ�⻬����O����ͬʱ�����ͷ���С�����������ƣ��������ٶ�Ϊg����С������Ĺ����У�����˵����ȷ���ǣ�������
��ͼ��ʾ����������Ϊm��A��BС��С����Ϊ�ʵ㣩��ͨ����Ϊl�IJ����쳤����ˮƽ�����������е�����·�H���̶�һ�⻬����O����ͬʱ�����ͷ���С�����������ƣ��������ٶ�Ϊg����С������Ĺ����У�����˵����ȷ���ǣ�������| A�� | �ӿ�ʼ���䵽�յ�����͵�Ĺ���AС��Ļ�е�ܲ��غ� | |
| B�� | �ӿ�ʼ���䵽�յ�����͵�Ĺ���A��BС����ܻ�е���غ� | |
| C�� | �����붤����ǰ˲�䣬AС���ܵ�������������СΪ$\frac{4mgH}{l}$ | |
| D�� | �����붤������˲�䣬AС���ܵ�������������СΪ$\frac{4mgH}{l}$ |
17������˵����ȷ���ǣ�������
| A�� | ϵͳ����������ʱ����һ������ | |
| B�� | Һ������������������ΪҺ��������Ӽ�ľ������Һ���ڲ����Ӽ�ľ��� | |
| C�� | �����˶���ӳ�˻���С�����ڲ����ӵ������˶� | |
| D�� | �ܱ����������һ�������������巢����ѹ����ʱ����λʱ����ײ���ڵ�λ��������������һ������ | |
| E�� | Ӱ�����������Լ�Ӱ�����ǶԸ�ˬ�볱ʪ���ܵ������ǿ�����ˮ������ѹǿ��ͬһ�¶���ˮ�ı�����ѹ�IJ�� |
7����ѧ���ǽ��ڷ�����һ�ž������1400�����ϵ�����ǡ�Kepler-452b������Χ����һ����̫������������ȵĺ������У����������ֵ���ӽ�����ġ���һ������һδ֪������������T������Kepler-452b���������뾶ΪR������Բ���˶���������������ΪG��������
| A�� | ���Լ����δ֪�����������Ϊ$\frac{{4{��^2}{R^3}}}{{G{T^2}}}$ | |
| B�� | ���ǡ�Kepler-452b���ĵ�һ�����ٶ�Ϊ$\sqrt{\frac{2��R}{T}}$ | |
| C�� | ���ǡ�Kepler-452b�����������������ٶ�Ϊ$\frac{{4{��^2}R}}{T^2}$ | |
| D�� | ���ǡ�Kepler-452b�����ܶ�Ϊ$\frac{3��}{{G{T^2}}}$ |
11�� ��ͼ��ʾ������ת��ǧ���е���������A��B������ȣ�ͨ����ͬ���ȵ�������������תԲ���ϣ������ǿ���������Ӱ�죬����תԲ������ֱ������������ת����A��B�ȶ�ʱ������˵����ȷ���ǣ�������
��ͼ��ʾ������ת��ǧ���е���������A��B������ȣ�ͨ����ͬ���ȵ�������������תԲ���ϣ������ǿ���������Ӱ�죬����תԲ������ֱ������������ת����A��B�ȶ�ʱ������˵����ȷ���ǣ�������
 ��ͼ��ʾ������ת��ǧ���е���������A��B������ȣ�ͨ����ͬ���ȵ�������������תԲ���ϣ������ǿ���������Ӱ�죬����תԲ������ֱ������������ת����A��B�ȶ�ʱ������˵����ȷ���ǣ�������
��ͼ��ʾ������ת��ǧ���е���������A��B������ȣ�ͨ����ͬ���ȵ�������������תԲ���ϣ������ǿ���������Ӱ�죬����תԲ������ֱ������������ת����A��B�ȶ�ʱ������˵����ȷ���ǣ�������| A�� | A���ٶȱ�B�Ĵ� | B�� | A��B�����ļ��ٶȴ�С��� | ||
| C�� | A��B�Ľ��ٶ���� | D�� | A��B������ƽ��̬ |




 ��ͼ��ʾ����������һ���ԴS������ƽ��ש�ϱ���Ĵ�ֱ����Ϊd������ש�ĺ��Ϊ$\frac{{\sqrt{3}}}{2}d$����S�����Ĺ���SA������Ǧ�=45�����䵽����ש�ϱ��棬��������ש����±����������֪�ش˹��ߴ����Ĺ�ӹ�ԴS������ש�ϱ���Ĵ���ʱ�����ڲ���ש�д���ʱ����ȣ���˲���ש��������n����Ӧ���ٽ��C��
��ͼ��ʾ����������һ���ԴS������ƽ��ש�ϱ���Ĵ�ֱ����Ϊd������ש�ĺ��Ϊ$\frac{{\sqrt{3}}}{2}d$����S�����Ĺ���SA������Ǧ�=45�����䵽����ש�ϱ��棬��������ש����±����������֪�ش˹��ߴ����Ĺ�ӹ�ԴS������ש�ϱ���Ĵ���ʱ�����ڲ���ש�д���ʱ����ȣ���˲���ש��������n����Ӧ���ٽ��C��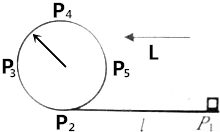 ��ͼ��ʾΪijͬѧ��Ƶġ��˶��糡��ģ��������ɽ����ʵ���ʾ��ͼ��ֱ���ε���P1P2��뾶ΪR��Բ���ε���ƽ��������P2������װ��ˮƽ̨���ϣ�������̨����̶�����������Ϊm��С��������磬�����ʼ�ձ���Ϊq����ˮƽ̨�����Գ��ٶ�v0��P1λ�ó������ص����˶���������Բ���˶���С������P1P2̨��Ķ�Ħ������Ϊ�̣����ಿ�ֵ�Ħ�����ƣ��������ٶ�Ϊg����ǿ�糡ˮƽ����ǿΪE����Eq�ݦ�mg��P1P2=l������С����ij��ٶȴ�С����������
��ͼ��ʾΪijͬѧ��Ƶġ��˶��糡��ģ��������ɽ����ʵ���ʾ��ͼ��ֱ���ε���P1P2��뾶ΪR��Բ���ε���ƽ��������P2������װ��ˮƽ̨���ϣ�������̨����̶�����������Ϊm��С��������磬�����ʼ�ձ���Ϊq����ˮƽ̨�����Գ��ٶ�v0��P1λ�ó������ص����˶���������Բ���˶���С������P1P2̨��Ķ�Ħ������Ϊ�̣����ಿ�ֵ�Ħ�����ƣ��������ٶ�Ϊg����ǿ�糡ˮƽ����ǿΪE����Eq�ݦ�mg��P1P2=l������С����ij��ٶȴ�С����������